Murtoluvut, prosenttiluvut ja suhdeluvut Osa A: murtolukujen kerto-ja Jakomallit (45 minuuttia)

BY admin
|

tässä osassa: pinta-Alamalli kertolaskua varten
aiemmin olet ehkä oppinut murtolukujen kerto-ja jakomalleja. Aiomme nyt käyttää joitakin visuaalisia malleja, joita olemme käyttäneet aiemmin tällä kurssilla ymmärtääksemme paremmin, mitä todella tapahtuu, kun suoritamme näitä operaatioita. KS. Huomautus 2 jäljempänä.

ensin käytämme aluemallia — sellaista, jossa päällekkäin on neliöitä, jotka on jaettu sopivaan määrään alueita ja varjostettu tarpeen mukaan — selventääksemme, mitä tapahtuu, kun kerrotaan Murtoluvut. Esimerkiksi näin osoittaisimme ongelman aluemallilla 3/8 • 2/3:

varjostaa yksi neliö, jaettu pystysuunnassa, edustaa 3/8 (alla vaaleanpunainen): varjosta toinen neliö, jaettu vaakasuoraan, edustaa 2/3 (alla sinisellä): aseta kaksi ruutua päällekkäin. Tuote on alue, joka on kaksinkertainen varjostettu (alla violetti):

mikä on tämän purppuranpunaisen alueen arvo? Violetteja osia on yhteensä 3 • 2 eli 6 kappaletta 8 * 3: sta eli 24: stä, joten violetin alueen arvo on 6/24.

tämä malli havainnollistaa visuaalisesti tutun algoritmin: kerrotaan kaksi murtolukua, kerrotaan osoittajat ja sitten kerrotaan nimittäjät. Tämä algoritmi ”laskee” sekä violetit osat (kahden osoittajan tulo) että osien kokonaismäärä (kahden nimittäjän tulo).

tätä mallia voidaan käyttää myös murtoluvun ”pienentämiseen”. Ensin vaihdamme joidenkin violettien osien asentoja. Kaksi purppuranpunaista osaa voidaan siirtää yläosaan, ja näin ollen kaksi kahdeksannesta osasta on nyt tummennettuja. Nämä kaksi kahdeksasosaa ovat samaa aluetta kuin neljännes:

tässä osassa: Kokeile itse
Tee omat neliökuultosi päällekkäin ja mallita ratkaisu jokaiseen vaiheeseen ongelmassa A1 alla.

ongelma A1
ilmakuvassa viljelysmaasta näkyy kolmen pellon mitat Mailin murto-osina. Käytä juuri oppimaasi pinta-alamallia mallintaaksesi kunkin näistä kentistä pinta-ala neliökilometreinä:
a. 3/4 * 1/3
b. 3/5 * 2/3
c. 1/4 • 8/9

ongelma A2
kuvaa, miten aluemalli osoittaa, että kahden positiivisen murtoluvun, joista kukin on pienempi kuin 1, tulon on oltava pienempi kuin jommankumman murtoluvun.

Videosegmentti
tässä segmentissä Jeanne ja Liz käyttävät aluemallia murtolukujen kertomiseen. He liittävät tämän mallin kertolaskualgoritmiin ja tarkistavat tapoja visuaalisesti vähentää murtolukuja. Katso tämä video segmentti, kun olet suorittanut ongelmia A1 ja A2.

tämä pätkä löytyy session videolta noin 4 minuuttia ja 32 sekuntia Annenbergin Medialogon jälkeen.

tässä osassa: Aluemalli Jakojäännökselle
voimme soveltaa aluemallia murtolukujen kertolaskuun havainnollistaaksemme kahden murtoluvun jakolaskun, kun kumpikin on pienempi kuin 1. Mallintaaksemme jakolaskun murtoluvuilla, käännämme enemmän tai vähemmän kertolaskussa käytetyn prosessin. Aloitamme etsimästämme alueesta ja löydämme yhden puuttuvista tekijöistä, joka muodostaa tuon alueen. KS. Huomautus 3 jäljempänä.

esimerkiksi näin mallia käyttäisimme ongelman osoittamiseen 1/4 2/3:

varjoa yksi neliö, jaettu pystysuunnassa, edustamaan 1/4 (kuten kertolaskumallissa, se on varjostettu violetti): päällekkäin neliön jaettu kolmanneksiin, sijoitettu vaakasuoraan, päälle neljäsosaa neliö, ja piirtää kiinnike oikealle kolmanneksesta neliö näyttää koko 2/3:

mitä näet nyt on violetti (1/4) alue ja koko yksi tekijä, joka teki kyseisen alueen.

tiedämme kertolaskumallista, että tulo 2/3 ja toinen tekijä (osamäärä) määrittelee pinta-alan, joka vastaa kooltaan 1/4: ää. Osamäärän löytämiseksi on liikuteltava violetin alueen yläosaa niin, että se on yhtä korkea kuin 2/3-kerroin.

Subdivide neljäsosaa neliö tehdä kahdeksasosa neliö: siirrä kaksi ylintä violettia kappaletta 2/3-korkeusalueelle (2/3-kiinnikkeen sisällä oleva alue): nyt varjostaa suorakulmioita heti oikealle ja välittömästi violetin alueen yläpuolelle:

tämä osoittaa, että 8 • 3: sta eli 24: stä osasta on 3 * 2 eli 6 violettia osaa. Violetti alue on 1/4, ja se tuli 2/3: sta kerrottuna millä? Toinen tekijä on 3/8.

ongelma A3
kaupunki aikoo rakentaa yhteisöpuutarhan, jonka pinta-ala olisi 2/3 neliökilometriä. He haluaisivat sijoittaa sen vanhan hevostilan laitumelle. Yksi ulottuvuus puutarha-alue määräytyy aita, joka on 3/4 kilometrin pitkä. Jakoalueen aluemallin avulla voit määrittää uuden puutarha-alueen toisen ulottuvuuden.

ongelma A4
kuvaa, miten aluemalli osoittaa, että kahden positiivisen murtoluvun, joista kukin on pienempi kuin 1, osamäärän on oltava suurempi kuin ensimmäinen murtoluku.

Tässä Osassa: Jakauman yhteinen Nimittäjämalli
murtolukujen jakamisen aluemalli ei auta havainnollistamaan, miksi meille tutuin algoritmi (käännä jakaja ja kerro sitten) toimii. Valitettavasti mikään malli ei voi näyttää sitä. KS. Huomautus 4 jäljempänä.

mutta tässä on erilainen jakoalgoritmi, jonka voimme selittää mallilla: Etsi yhteinen nimittäjä, etsi ekvivalentit Murtoluvut ja jaa osoittajat.

jotta ymmärtäisimme tämän algoritmin mallin, palataan ensin tarkastelemaan joitakin jakokäsitteitä. On yleensä helpompi laskea, jos ajattelee jakoa quotatiivisesti. Näin voidaan sanoa, että 6 3 kysyy: ”montako kolmosta on 6: ssa?”

seuraavaksi on ymmärrettävä yksiköiden rooli divisioonassa.

ongelma A5
mikä näistä kysymyksistä mahdollisesti antaa toisenlaisen vastauksen?
* kuinka monta kolmosta on 6: ssa?
* kuinka monta ryhmää 3 kymppiä on 6 kymmenessä?
* kuinka monta kolmen viitosen ryhmää on 6 Vitosessa?
* kuinka monta kolmen kymmenesosan ryhmää on 6 kymmenesosassa?* Kuinka monta ryhmää 3 @s On olemassa 6 @s?
* kuinka monta ryhmää 3 anythings on olemassa 6 anythings (kunhan molemmat anythings viittaavat samaan yksikköön)?

tässä on kyse siitä, että ongelman yksiköillä ei ole merkitystä — jos yksiköt ovat sama kokonaisuus, ne häviävät jaettaessa.

tämä tuo meidät takaisin uuteen algoritmiin jakamiselle murtoluvuilla: jaetaan kaksi murtolukua, etsitään yhteinen nimittäjä ja jaetaan sitten osoittajat.

kokeillaan visuaalista versiota ongelmasta, jonka teimme aiemmin: 1/4 2/3. Etsi ensin yhteinen nimittäjä:

1/4 2/3 = 3/12 8/12

Jaa seuraavaksi osoittajat:

38 = 3/8

tässä on malli tähän ongelmaan, jota kutsutaan yhteisen nimittäjän malliksi:

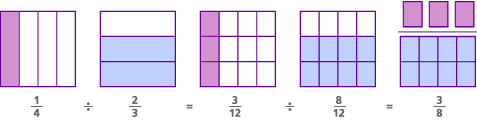
tässä ongelmassa, itse asiassa, alkuperäinen kysymys oli ” kuinka monta 2 / 3s on olemassa 1 / 4?”Löytämällä yhteisen nimittäjän muutimme kysymyksen” Kuinka monta 8 / 12: ta on 3/12: ssa?”- mikä on sama kuin kysyä ” kuinka monta 8: aa on 3: ssa?”Vastaus molempiin kysymyksiin on sama:” on 3/8 8: sta 3: sta.”

ongelma A6
käytä yhteisen nimittäjän mallia jakaaksesi 3/5 3/4: llä.

ongelma A7
miksi 0, 6 0, 2 on sama vastaus kuin 6 2?

tässä osassa: prosessin kääntäminen desimaaleiksi
voit laajentaa sen, mitä olet oppinut operaatioista ja murtoluvuista, myös desimaaleiksi. Muista, että päättyvä desimaali voidaan ajatella murtoluvuksi, jonka potenssi on 10 nimittäjänä (esim.0,4 = 4/10). KS. Huomautus 5 jäljempänä.

miksi desimaalipilkkuja pitää rivittää, kun desimaaleja lisätään tai vähennetään?
meidän täytyy rivittää desimaalipilkut, koska voimme lisätä tai vähentää vain, jos yksiköt ovat samat. Yhdenmukaistamalla desimaalipisteitä varmistamme, että lisäämme tai vähennämme numeroita, joilla on samat paikkamäärät, aivan kuten teemme, kun lisäämme tai vähennämme kokonaislukuja.

miksi lasketaan desimaalit, kun kerrotaan desimaalit?
Session 3 eksponentteja koskevasta osiosta tiedämme, että kertolasku eksponenteilla vaatii eksponenttien yhteenlaskua eli ”laskemista”. Niinpä esimerkiksi 0,2 • 0,03 eksponentiaalisessa muodossa on seuraava:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

eksponentit ovat -1 ja -2, jotka ovat yksi ja kaksi paikkaa vastaavasti desimaalipilkun oikealla puolella. Tällöin tuotteella on eksponentti, joka on lukujen -1 ja -2 summa (eli -3), ja on kolme paikkaa desimaalipilkun oikealla puolella. 0,2 • 0,03: n tuote on 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

miksi siirrämme desimaaleja, kun jaamme desimaaleja?
tämä prosessi liittyy ekvivalenttien murtolukujen löytämiseen. Jakoa voi pitää murtolukuna. Koska ongelma 2,5 0.05 on vaikea visualisoida, kirjoita se 2.5 / 0.05. Tarvitset nimittäjään kokonaisluvun, joten kerro 100: lla saadaksesi kokonaisluvun. Kompensoidaksesi nimittäjän kertomisen 100: lla, sinun on myös kerrottava Osoittaja 100: lla. Se tarkoittaa, että kerrottuna 100/100: lla eli 1: llä, joka ei muuta murtoluvun arvoa. Tältä prosessi näyttää: