törtek, százalékok és arányok A. rész: törtek szorzásának és osztásának modelljei (45 perc)

ebben a részben: Területmodell a szorzáshoz
a múltban megtanulhatott bizonyos algoritmusokat a törtek szorzására és osztására. Most néhány olyan vizuális modellt fogunk használni, amelyeket korábban alkalmaztunk ebben a kurzusban, hogy jobban megértsük, mi történik valójában, amikor ezeket a műveleteket végrehajtjuk. Lásd az alábbi 2. megjegyzést.

először egy olyan területmodellt fogunk használni, amely a megfelelő számú régióra particionált és szükség szerint árnyékolt négyzeteket egymásra helyezi, hogy tisztázza, mi történik a törtek szorzásakor. Például a következő módon használnánk a területmodellt a probléma bemutatására 3/8 • 2/3:

árnyékoljon egy négyzetet, függőlegesen felosztva, hogy képviselje a 3/8-ot (az alábbiakban rózsaszínben látható):		árnyékoljon egy másik négyzetet, vízszintesen felosztva, hogy képviselje a 2/3-ot (az alábbiakban kék színnel látható):		helyezze rá a két négyzetet. A termék a kettős árnyékolású terület (az alábbiakban lila színnel látható):

mi az értéke ennek a lila területnek? 3 • 2 vagy 6 Lila rész van a 8 * 3-ból, vagy 24-ből, tehát a lila terület értéke 6/24.

ez a modell vizuálisan bemutatja az ismerős algoritmust: két frakció szorzásához szorozzuk meg a számlálókat, majd szorozzuk meg a nevezőket. Ez az algoritmus” megszámolja ” mind a lila részeket (a két számláló szorzatát), mind az alkatrészek teljes számát (A két nevező szorzatát).

ezt a modellt a frakció “csökkentésére” is használhatjuk. Először kicseréljük néhány lila rész helyzetét. A lila részek közül kettő a tetejére mozgatható, így a nyolcad közül kettő árnyékos. Ez a két nyolcad ugyanaz a terület, mint egy negyed:

ebben a részben: próbáld ki magad
Készíts saját négyzetes fóliákat az egymásra helyezéshez, és modellezd a megoldást az alábbi A1 probléma minden egyes lépéséhez.

probléma A1
a mezőgazdasági területekről készült légifotó három mező méretét mutatja mérföldes töredékekben. Használja az imént megtanult területmodellt a terület négyzetmérföldben történő modellezéséhez:
a. 3/4 * 1/3
b. 3/5 * 2/3
c. 1/4 • 8/9

probléma A2
írja le, hogy a területmodell hogyan mutatja, hogy két pozitív frakció szorzatának, amelyek mindegyike kevesebb, mint 1, kisebbnek kell lennie, mint bármelyik frakció.

videó szegmens
ebben a szegmensben Jeanne és Liz a területmodellt használja a frakciók szorzására. Ezt a modellt a szorzási algoritmushoz kapcsolják, és ellenőrzik a frakciók vizuális csökkentésének módjait. Nézze meg ezt a videó szegmenst, miután befejezte az A1 és A2 problémákat.

ezt a részt az Annenberg Media logó után körülbelül 4 perccel és 32 másodperccel találja meg a session videón.

ebben a részben: Területmodell osztáshoz
alkalmazhatjuk a területmodellt a frakciók szorzására, hogy két frakció osztását vizualizáljuk, ha mindegyik kisebb, mint 1. A frakciókkal való osztás modellezéséhez többé-kevésbé megfordítjuk a szorzáshoz használt folyamatot. Egy keresett területtel kezdjük, és megtaláljuk az egyik hiányzó tényezőt, amely ezt a területet alkotja. Lásd az alábbi 3. megjegyzést.

például a következőképpen mutatjuk be a modellt a probléma bemutatására 1/4 2/3:

árnyékoljon egy négyzetet, függőlegesen felosztva, hogy képviselje az 1/4-et (mint a szorzási modellben, árnyékolt lila):		helyezzen rá egy harmadra osztott, vízszintesen elhelyezett négyzetet a negyedik négyzetre, majd rajzoljon egy zárójelet a harmadok négyzetétől jobbra, hogy megmutassa a 2/3 méretét:

amit most lát, az a lila (1/4) terület és az egyik tényező mérete, amely ezt a területet létrehozta.

a szorzási modellből tudjuk, hogy a 2/3 szorzata és egy másik tényező (a hányados) 1/4-nek megfelelő méretű területet határoz meg. A hányados megtalálásához a lila terület felső részét úgy kell mozgatnunk, hogy ugyanolyan magas legyen, mint a 2/3 tényező.

ossza fel a negyedik négyzetet, hogy egy nyolcadik négyzetet készítsen:		mozgassa a felső két lila darabot a 2/3 magasságú területre (a 2/3 konzolon belüli területre):		most árnyékolja a téglalapokat közvetlenül jobbra, közvetlenül a lila terület fölé:

ez azt mutatja, hogy összesen 3 • 2 vagy 6 Lila rész van a 8 * 3-ból, vagy 24-ből. A lila terület egyenlő 1/4-gyel, és a 2/3 szorzatából származik, és mivel szorozva? Láthatjuk, hogy a másik tényező 3/8.

probléma A3
egy város közösségi kert építését tervezi, amely egy négyzetmérföld 2/3-át lefedi. Egy régi lófarm legelőjén szeretnék elhelyezni. A kert területének egyik dimenzióját egy mérföld hosszú, 3/4-es kerítés határozza meg. Használja a területmodellt az osztáshoz az új kertterület másik dimenziójának meghatározásához.

probléma A4
írja le, hogy a területmodell hogyan mutatja, hogy két pozitív frakció hányadosának, amelyek mindegyike kevesebb, mint 1, nagyobbnak kell lennie, mint az első frakció.

Ebben A Részben: Az Osztás Közös Nevező modellje
a törtek felosztásának területmodellje nem segít annak szemléltetésében, hogy miért működik a legjobban ismert algoritmus (az osztó megfordítása, majd szorzása). Sajnos ezt egyetlen modell sem tudja megmutatni. Lásd az alábbi 4. megjegyzést.

de itt van egy másik osztási algoritmus, amelyet egy modellel meg tudunk magyarázni: keresse meg a közös nevezőt, keresse meg az ekvivalens törteket, és ossza el a számlálókat.

annak érdekében, hogy megértsük ennek az algoritmusnak a modelljét, először térjünk vissza a felosztás néhány fogalmának áttekintésére. Általában könnyebb kiszámítani, ha idéző módon gondolkodik az osztásról. Így azt mondhatjuk, hogy 6 3 megkérdezi: “hány 3 van a 6-ban?”

ezután meg kell értenünk az egységek szerepét a divízióban.

probléma A5
e kérdések közül melyik ad más választ, ha van ilyen?

a lényeg itt az, hogy a probléma egységei nem számítanak — ha az egységek ugyanazok az entitások, akkor eltűnnek, amikor megosztod.

ez visszavezet minket a törtekkel való osztás új algoritmusához: két frakció felosztásához keressen egy közös nevezőt, majd ossza meg a számlálókat.

próbáljuk meg a probléma vizuális változatát, amelyet korábban tettünk: 1/4 2/3. Először keressen egy közös nevezőt:

1/4 2/3 = 3/12 8/12

ezután ossza meg a számlálókat:

38 = 3/8

itt van a probléma modellje, az úgynevezett közös nevező modell:

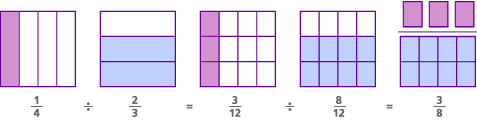
ebben a problémában valójában az eredeti kérdés az volt, hogy “hány 2/3 van 1/4-ben?”A közös nevező megtalálásával megváltoztattuk a kérdést: “Hány 8/12 van 3/12-ben?— – ami megegyezik azzal a kérdéssel, hogy ” hány 8-as van 3-ban?”A válasz mindkét kérdésre ugyanaz:” van 3/8 egy 8 a 3-ban.”

probléma A6
használja a közös nevező modellt a 3/5 elosztására 3/4-gyel.

probléma A7
miért 0,6 0,2 ugyanazt a választ, mint 6 2?

ebben a részben: a folyamat fordítása Tizedesjegyekre
a műveletekről és törtekről tanultakat tizedesjegyekre is kiterjesztheti. Ne feledje, hogy a végződő tizedesjegyet úgy lehet elképzelni, mint egy 10-es teljesítményű frakciót, mint nevezőt (például 0,4 = 4/10). Lásd az alábbi 5. megjegyzést.

miért kell a tizedesjegyeket összeadni vagy kivonni?
a tizedeseket sorba kell állítanunk, mert csak akkor tudunk összeadni vagy kivonni, ha az egységek azonosak. A tizedesjegyek igazításával megbizonyosodunk arról, hogy olyan számjegyeket adunk hozzá vagy vonunk le, amelyek azonos helyértékekkel rendelkeznek, ugyanúgy, mint egész számok összeadásakor vagy kivonásakor.

miért számoljuk a tizedesjegyeket, amikor tizedesjegyeket szorozunk?
a 3.szekció kitevőkről szóló szakaszából tudjuk, hogy a kitevőkkel való szorzás megköveteli a kitevők hozzáadását vagy “számlálását”. Tehát például 0,2 * 0,03 az exponenciális formában a következő:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

a kitevők -1 és -2, amelyek egy, illetve két helyen vannak a tizedesvesszőtől jobbra. A szorzatnak ekkor lesz egy kitevője, amely -1 és -2 (azaz -3) összege, és három hellyel jobbra van a tizedesvesszőtől. A 0,2 • 0,03 szorzata 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

miért mozgatjuk a tizedesjegyeket, amikor tizedesjegyekkel osztjuk?
ez a folyamat egyenértékű frakciók megtalálásához kapcsolódik. Gondolhat a felosztásra, mint egy töredékre. Mivel a probléma 2,5 0.A 05-öt nehéz megjeleníteni, írja be 2,5/0,05-ként. Szüksége van egy egész számra a nevezőben, ezért szorozza meg 100-zal, hogy egész számot kapjon. A nevező 100-as szorzásának kompenzálásához a számlálót is meg kell szorozni 100-mal. Ez azt jelenti, hogy valójában megszoroztad 100/100-mal vagy 1-gyel, ami nem változtatja meg a tört értékét. Így néz ki a folyamat: