Frazioni, Percentuali, proporzioni e Parte A: Modelli per la Moltiplicazione e Divisione di Frazioni (45 minuti)

BY admin
|

In Questa Parte: l’Area del Modello per la Moltiplicazione
In passato, si può avere imparato particolari algoritmi per la moltiplicazione e divisione di frazioni. Ora useremo alcuni dei modelli visivi che abbiamo impiegato in precedenza in questo corso per capire meglio cosa sta realmente accadendo quando eseguiamo queste operazioni. Vedi Nota 2 qui sotto.

Per prima cosa useremo un modello di area — uno che sovrappone i quadrati che sono partizionati nel numero appropriato di regioni e ombreggiati secondo necessità — per chiarire cosa succede quando si moltiplicano le frazioni. Per esempio, ecco come si può utilizzare il modello di area per illustrare il problema 3/8 • 2/3:

Ombra di una piazza, divisa verticalmente, per rappresentare 3/8 (mostrato di seguito in rosa): Ombra un’altra piazza, divisa orizzontalmente, che rappresentano i 2/3 (evidenziati in blu): Sovrapporre le due piazze. Il prodotto è l’area che è il doppio di ombreggiata (mostrato di seguito in viola):

Qual è il valore di questa area viola? Ci sono 3 * 2, o 6, parti viola su 8 * 3, o 24, parti in tutto, quindi il valore dell’area viola è 6/24.

Questo modello dimostra visivamente l’algoritmo familiare: per moltiplicare due frazioni, moltiplicare i numeratori e quindi moltiplicare i denominatori. Questo algoritmo “conta” sia le parti viola (il prodotto dei due numeratori) che il numero totale di parti (il prodotto dei due denominatori).

Possiamo anche usare questo modello per “ridurre” la frazione. Per prima cosa scambiamo le posizioni di alcune delle parti viola. Due delle parti viola possono essere spostate verso l’alto e, quindi, due degli ottavi sono ora ombreggiati. Questi due ottavi sono la stessa area di un quarto:

In questa parte: Provalo tu stesso
Crea le tue trasparenze quadrate da sovrapporre e modella la soluzione per ogni passaggio nel problema A1 di seguito.

Problema A1
Una foto aerea di terreni agricoli mostra le dimensioni di tre campi in frazioni di miglio. Usa il modello di area che hai appena imparato per modellare l’area in miglia quadrate di ciascuno di questi campi:
a. 3/4 • 1/3
b. 3/5 • 2/3
c. 1/4 • 8/9

Problema A2
Descrivere come il modello di area mostra che il prodotto di due frazioni positive, ciascuna inferiore a 1, deve essere più piccolo di una delle frazioni.

Segmento video
In questo segmento, Jeanne e Liz usano il modello di area per moltiplicare le frazioni. Mettono in relazione questo modello con l’algoritmo di moltiplicazione e controllano i modi per ridurre visivamente le frazioni. Guarda questo segmento video dopo aver completato i problemi A1 e A2.

È possibile trovare questo segmento nel video della sessione circa 4 minuti e 32 secondi dopo il logo Annenberg Media.

In questa parte: Modello di area per la divisione
Possiamo applicare il modello di area per la moltiplicazione delle frazioni per visualizzare la divisione di due frazioni quando ciascuna è inferiore a 1. Per modellare la divisione con le frazioni, invertiamo più o meno il processo utilizzato per la moltiplicazione. Iniziamo con un’area che stiamo cercando, e troviamo uno dei fattori mancanti che compongono quell’area. Vedi Nota 3 qui sotto.

Per esempio, ecco come si può utilizzare il modello per illustrare il problema 1/4 2/3:

Ombra di una piazza, divisa verticalmente, per rappresentare 1/4 (come nella moltiplicazione modello, è viola sfumato): Sovrapporre un quadrato diviso in terzi, posizionata orizzontalmente, sulla quarta piazza, e disegnare una staffa per il diritto dei terzi piazza per mostrare la dimensione di 2/3:

Quello che vedi ora è l’area viola (1/4) e la dimensione di uno dei fattori che hanno creato quell’area.

Sappiamo dal modello di moltiplicazione che il prodotto di 2/3 e un altro fattore (il quoziente) definisce un’area di dimensioni equivalenti a 1/4. Per trovare il quoziente, dobbiamo spostare la parte superiore dell’area viola in modo che sia la stessa altezza del fattore 2/3.

Suddividere il quarto quadrato per fare un ottavo quadrato: Spostare il top porpora due pezzi in 2/3 dell’altezza (l’area entro i 2/3 staffa): Adesso ombreggiano i rettangoli subito a destra e subito al di sopra dell’area viola:

Questo dimostra che ci sono 3 • 2, o 6, viola le parti di 8 • 3 o 24, in tutte le parti. L’area viola è uguale a 1/4, e proviene dal prodotto di 2/3 moltiplicato per cosa? Possiamo vedere che l’altro fattore è 3/8.

Problema A3
Una città prevede di costruire un giardino comunitario che coprirà 2/3 di miglio quadrato. Vorrebbero collocarlo su un pascolo di un vecchio allevamento di cavalli. Una dimensione dell’area del giardino sarà determinata da una recinzione lunga 3/4 di miglio. Utilizzare il modello di area per la divisione per determinare l’altra dimensione della nuova area del giardino.

Problema A4
Descrivere come il modello di area mostra che il quoziente di due frazioni positive, ciascuna inferiore a 1, deve essere maggiore della prima frazione.

In questa parte: Il modello del denominatore comune per la divisione
Il modello di area per la divisione delle frazioni non aiuta a illustrare perché l’algoritmo con cui abbiamo più familiarità (inverti il divisore e quindi moltiplica) funziona. Sfortunatamente, nessun modello può dimostrarlo. Vedi Nota 4 qui sotto.

Ma ecco un algoritmo di divisione diverso, che possiamo spiegare con un modello: trova il denominatore comune, trova le frazioni equivalenti e dividi i numeratori.

Per comprendere il modello di questo algoritmo, torniamo prima a rivedere alcuni dei concetti di divisione. Di solito è più facile da calcolare se si pensa alla divisione in modo quotativo. Quindi, puoi dire che 6 3 chiede: “Quanti 3 ci sono in 6?”

Successivamente, dobbiamo capire il ruolo delle unità nella divisione.

Problema A5
Quale, se esiste, di queste domande produce una risposta diversa?

Il punto qui è che le unità del problema non contano — se le unità sono la stessa entità, scompaiono quando si divide.

Questo ci riporta al nuovo algoritmo per la divisione con le frazioni: dividere due frazioni, trovare un denominatore comune e quindi dividere i numeratori.

Proviamo una versione visiva del problema che abbiamo fatto prima: 1/4 2/3. In primo luogo, trovare un denominatore comune:

1/4 2/3 = 3/12 8/12

Quindi, dividi i numeratori:

38 = 3/8

Ecco il modello per questo problema, chiamato modello comune denominatore:

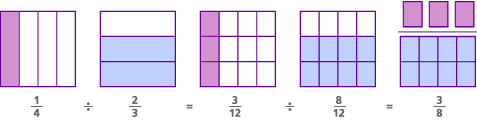
In questo problema, in effetti, la domanda originale era ” Quanti 2 / 3 ci sono in 1/4?”Trovando un denominatore comune, abbiamo cambiato la domanda in” Quanti 8 / 12 ci sono in 3 / 12?”- che è lo stesso di chiedere ” Quanti 8 ci sono in 3?”La risposta a entrambe le domande è la stessa:” C’è 3/8 di un 8 in 3.”

Problema A6
Usa il modello del denominatore comune per dividere 3/5 per 3/4.

Problema A7
Perché 0.6 0.2 ha la stessa risposta di 6 2?

In questa parte: Traducendo il processo in decimali
Puoi estendere ciò che hai imparato sulle operazioni e le frazioni anche ai decimali. Ricorda che un decimale terminante può essere pensato come una frazione con una potenza di 10 come denominatore (ad esempio, 0.4 = 4/10). Vedi Nota 5 qui sotto.

Perché abbiamo bisogno di allineare i punti decimali quando aggiungiamo o sottraiamo decimali?
Dobbiamo allineare i punti decimali perché possiamo solo aggiungere o sottrarre se le unità sono le stesse. Allineando i punti decimali, ci assicuriamo che stiamo aggiungendo o sottraendo cifre che hanno gli stessi valori di posto, proprio come facciamo quando aggiungiamo o sottraiamo numeri interi.

Perché contiamo le cifre decimali quando moltiplichiamo i decimali?
Dalla sezione sugli esponenti nella sessione 3, sappiamo che la moltiplicazione con gli esponenti richiede l’aggiunta o il “conteggio” degli esponenti. Quindi, ad esempio, 0,2 * 0,03 nella forma esponenziale è il seguente:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

Gli esponenti sono -1 e -2, che sono uno e due posti, rispettivamente, a destra del punto decimale. Il prodotto avrà quindi un esponente che è la somma di -1 e -2 (cioè, -3), ed è tre posti a destra del punto decimale. Il prodotto di 0.2 • 0.03 è 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

Perché spostiamo i punti decimali quando dividiamo con i decimali?
Questo processo è correlato alla ricerca di frazioni equivalenti. Puoi pensare alla divisione come a una frazione. Dal momento che il problema 2.5 0.05 è difficile da visualizzare, scrivilo come 2.5 / 0.05. Hai bisogno di un numero intero nel denominatore, quindi moltiplica per 100 per ottenere un numero intero. Per compensare la moltiplicazione del denominatore per 100, devi anche moltiplicare il numeratore per 100. Ciò significa che in realtà moltiplicato per 100/100, o 1, che non cambia il valore della frazione. Ecco come appare il processo: