分数、パーセント、および比率パートA:分数の乗算と除算のためのモデル(45分)

このパートで:乗算のための面積モデル
過去には、分数の乗算と除算のための特定のアルゴリズムを学んだことがあるかもしれません。 ここでは、これらの操作を実行するときに実際に何が起こっているのかをよりよく理解するために、このコースで以前に採用したいくつかの視覚モデ 以下の注2を参照してください。

まず、適切な数の領域に分割され、必要に応じて網掛けされた正方形を重ね合わせる面積モデルを使用して、分数を乗算するとどうなるかを明確にします。 たとえば、領域モデルを使用して問題を実証する方法は次のとおりです3/8 • 2/3:

3/8を表すために、垂直に分割された一つの正方形を陰にします（下にピンクで示されています):		2/3を表すために、水平に分割された別の正方形を陰にします（下に青で示します):		二つの正方形を重ね合わせます。 製品は、二重の網掛けされた領域です（下に紫色で表示されています）。):

この紫色の領域の価値は何ですか？ 3•2、または6、8•3、または24、すべての部分のうち紫色の部分があるので、紫色の領域の値は6/24です。

このモデルは、使い慣れたアルゴリズムを視覚的に示しています。 このアルゴリズムは、紫色の部分（2つの分子の積）と部品の総数（2つの分母の積）の両方を「カウント」します。

このモデルを使用して分数を”減らす”こともできます。 まず、紫色の部分のいくつかの位置を交換します。 紫色の部分の2つは上に移動することができ、したがって、8分の2は現在網掛けされています。 これら二つの八分の一は四分の一と同じ面積です:

この部分では、自分で試してみてください
重ね合わせるために独自の正方形の透明度を作成し、以下の問題A1の各ステップの解をモデル化します。

問題A1
農地の航空写真は、マイルの分数で三つのフィールドの寸法を示しています。 次の各フィールドの平方マイルで面積をモデル化する方法を学習したエリアモデルを使用します。
a.3/4•1/3
b.3/5•2/3
c. 1/4 • 8/9

問題A2
は、面積モデルが、それぞれが1未満の二つの正の分数の積がいずれかの分数よりも小さくなければならないことをどのように示している

ビデオセグメント
このセグメントでは、JeanneとLizは面積モデルを使用して分数を乗算します。 彼らはこのモデルを乗算アルゴリズムに関連付け、分数を視覚的に減らす方法をチェックします。 問題A1とA2を完了した後、このビデオセグメントを見てください。

このセグメントは、Annenberg Mediaロゴの約4分32秒後のセッションビデオで見つけることができます。

この部分では、除算の面積モデル
分数の乗算の面積モデルを適用して、それぞれが1未満のときに二つの分数の除算を視覚化することができます。 分数で除算をモデル化するには、乗算に使用されるプロセスを多かれ少なかれ逆にします。 私たちが探している領域から始め、その領域を構成する不足している要因の1つを見つけます。 以下の注3を参照してください。

たとえば、このモデルを使用して問題を実証する方法は次のとおりです1/4 2/3:

1/4を表すために、垂直に分割された1つの正方形を陰影付けします（乗算モデルのように、紫色の陰影付けがされています):		三分の一に分割され、水平に配置された正方形を四分の一の正方形の上に重ね合わせ、三分の一の正方形の右側にブラケットを描画して2/3の大きさを示:

あなたが今見ているのは、紫色（1/4）の領域とその領域を作った要因の1つのサイズです。

乗算モデルから、2/3と別の因子（商）の積が1/4に相当する面積を定義することがわかります。 商を見つけるには、紫色の領域の上部を移動して、2/3因子と同じ高さにする必要があります。

八分の一の正方形を作るために四分の一の正方形を細分化します:		上の2つの紫色の部分を2/3の高さの領域（2/3ブラケット内の領域）に移動します):		今すぐ右にすぐに、すぐに紫色の領域の上に長方形を陰にします:

これは、3•2、または6、8•3、または24、すべての部分のうち紫色の部分があることを示しています。 紫色の領域は1/4に等しく、2/3の積に何を掛けたのですか？ 私たちは、他の要因が3/8であることがわかります。

問題A3
町は平方マイルの2/3をカバーするコミュニティガーデンを建設する予定です。 彼らは古い馬の農場の牧草地にそれを配置したいと思います。 庭区域の1つの次元はマイルの長さの3/4である塀によって定められる。 分割の面積モデルを使用して、新しい庭の面積の他の次元を決定します。

問題A4
面積モデルが、それぞれが1未満の二つの正の分数の商が最初の分数より大きくなければならないことをどのように示しているかを説

: 除算の共通分母モデル
分数の除算の面積モデルは、私たちが最も精通しているアルゴリズム（除数を反転して乗算）が機能する理由を説明するのに役 残念ながら、モデルはそれを示すことはできません。 以下の注4を参照してください。

しかし、ここでは別の除算アルゴリズムがあり、モデルで説明できます：共通分母を見つけ、同等の分数を見つけ、分子を分割します。

このアルゴリズムのモデルを理解するために、最初に分割の概念のいくつかを見直すことに戻りましょう。 通常、除算について見積もり的な方法で考えると、計算が簡単です。 したがって、63は、”6にはいくつの3がありますか？”

次に、部門におけるユニットの役割を理解する必要があります。

問題A5
これらの質問のうち、どちらが異なる答えをもたらすのでしょうか？
•6には3が何個ありますか？
•6十の中に3十のグループは何個ありますか？
•6つのファイブには3つのファイブのグループが何組ありますか？
•6十分の3のグループは何個ありますか？•6@sには3@sのグループがいくつありますか？
•3つのanythingsのうち6つのanythingsにはいくつのグループがありますか（両方のanythingsが同じユニットを参照している限り）？

ここでのポイントは、問題の単位は問題ではないということです—単位が同じエンティティであれば、分割すると消えます。

これは、分数による除算のための新しいアルゴリズムに戻ります：二つの分数を分割するには、共通の分母を見つけてから分子を分割します。

以前に行った問題の視覚的なバージョンを試してみましょう：1/42/3。 まず、共通分母を見つける:

1/4 2/3 = 3/12 8/12

次に、分子を分割します:

38 = 3/8

ここでは、共通分母モデルと呼ばれるこの問題のモデルは、次のとおりです:

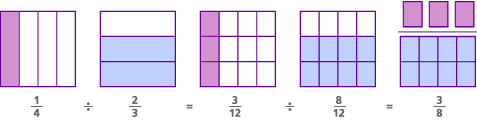
この問題では、実際には、元の質問は「1/4にいくつの2/3がありますか？「共通の分母を見つけることで、質問を「3/12には何人の8/12がありますか？”-これは、尋ねると同じです”どのように多くの8sが3にありますか？”両方の質問に対する答えは同じです：”3/8の8in3があります。”

問題A6
共通分母モデルを使用して3/5を3/4で除算します。なぜ0.60.2が62と同じ答えを持っているのですか？

この部分では、プロセスを小数に変換する
操作と分数について学んだことを小数に拡張することもできます。 終端の10進数は、分母として10の累乗を持つ分数と考えることができます（例えば、0.4=4/10）。 以下の注5を参照してください。

小数を加算または減算するときに小数点を並べる必要があるのはなぜですか？
単位が同じ場合にのみ加算または減算できるため、小数点を並べる必要があります。 小数点を整列させることで、整数を加算または減算するときと同じように、同じ場所の値を持つ数字を加算または減算していることを確認します。

小数を掛けるときに小数点以下の桁数を数えるのはなぜですか？
セッション3の指数に関するセクションから、指数との乗算には指数の加算または「カウント」が必要であることがわかります。 したがって、たとえば、指数形式の0.2•0.03は次のようになります:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

指数は-1と-2で、小数点の右側にそれぞれ1と2の場所があります。 この積は、-1と-2の合計（つまり-3）である指数を持ち、小数点の右側に3桁あります。 0.2•0.03の積は0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

小数で除算するときに小数点を移動するのはなぜですか？
このプロセスは、等価な分数を見つけることに関連しています。 除算は分数と考えることができます。 問題2.50以来。05は視覚化するのが難しいので、2.5/0.05と書いてください。 分母に整数が必要なので、整数を取得するには100を掛けます。 分母に100を掛けることを補正するには、分子にも100を掛ける必要があります。 つまり、実際には100/100または1を掛けたもので、分数の値は変更されません。 プロセスは次のようになります：