Fraksjoner, Prosent, Og Forholdstall Del A: Modeller For Multiplikasjon og Deling Av Fraksjoner (45 minutter)

BY admin
|

I Denne Delen: Area Model For Multiplikasjon
Tidligere har du kanskje lært spesielle algoritmer for multiplikasjon Og deling av fraksjoner. Vi skal nå bruke noen av de visuelle modellene vi har ansatt tidligere i dette kurset for å bedre forstå hva som faktisk skjer når vi utfører disse operasjonene. Se Note 2 nedenfor.

først bruker Vi en områdemodell — en som overlegger firkanter som er delt inn i riktig antall regioner — og skyggelagt etter behov – for å avklare hva som skjer når du multipliserer brøker. For eksempel, her er hvordan vi ville bruke området modellen for å demonstrere problemet 3/8 • 2/3:

Skygge en firkant, partisjonert vertikalt, for å representere 3/8 (vist nedenfor i rosa): Skygge en annen firkant, partisjonert horisontalt, for å representere 2/3 (vist nedenfor i blått): Legg Over de to rutene. Produktet er området som er dobbelt skyggelagt (vist nedenfor i lilla):

Hva er verdien av dette lilla området? Det er 3 * 2 eller 6 lilla deler ut av 8 • 3 eller 24 deler i det hele tatt, så verdien av det lilla området er 6/24.

denne modellen demonstrerer visuelt den kjente algoritmen: å multiplisere to fraksjoner, multiplisere telleren og deretter multiplisere denominatorene. Denne algoritmen «teller» både de lilla delene (produktet av de to tellerne) og det totale antall deler (produktet av de to betegnelsene).

vi kan også bruke denne modellen til å «redusere» fraksjonen. Først bytter vi posisjonene til noen av de lilla delene. To av de lilla delene kan flyttes til toppen, og dermed er to av åttende nå skyggelagt. Disse to åttende er det samme området som en fjerdedel:

I Denne Delen: Prøv Det Selv
Lag dine egne firkantede transparenter for å legge over, og modell løsningen for hvert trinn I Problem A1 nedenfor.

Problem A1
et luftfoto av jordbruksmark viser dimensjonene på tre felt i brøkdeler av en mil. Bruk områdemodellen du nettopp har lært å modellere området i square miles av hvert av disse feltene:
a. 3/4 * 1/3
b. 3/5 * 2/3
c. 1/4 • 8/9

Problem A2
Beskriv hvordan områdemodellen viser at produktet av to positive fraksjoner, hver mindre enn 1, må være mindre enn noen av fraksjonene.

Videosegment
I Dette segmentet bruker Jeanne Og Liz områdemodellen til å multiplisere brøker. De relaterer denne modellen til multiplikasjonsalgoritmen og ser etter måter å visuelt redusere fraksjoner på. Se dette videosegmentet etter At Du har fullført Problemene A1 og A2.

du finner dette segmentet på øktvideoen omtrent 4 minutter og 32 sekunder etter Annenberg Media-logoen.

I Denne Delen: Arealmodell For Divisjon
kan vi bruke arealmodellen for multiplikasjon av fraksjoner for å visualisere delingen av to fraksjoner når hver er mindre enn 1. For å modellere divisjon med brøker, reverserer vi mer eller mindre prosessen som brukes til multiplikasjon. Vi starter med et område vi leter etter, og vi finner en av de manglende faktorene som utgjør det området. Se Note 3 nedenfor.

for eksempel, Slik bruker vi modellen til å demonstrere problemet 1/4 2/3:

Skygge en firkant, partisjonert vertikalt, for å representere 1/4 (som i multiplikasjonsmodellen er den skyggelagt lilla): Legg over en firkant delt inn i tredjedeler, plassert horisontalt, på fjerdeplassen, og trekk en brakett til høyre for tredjeplassen for å vise størrelsen på 2/3:

Det du ser nå er det lilla (1/4) området og størrelsen på en av faktorene som gjorde dette området.

vi vet fra multiplikasjonsmodellen at produktet av 2/3 og en annen faktor (kvotienten) definerer et område tilsvarende i størrelse til 1/4. For å finne kvotienten må vi flytte den øverste delen av det lilla området slik at det er samme høyde som 2/3-faktoren.

Del opp fjerdeplassen for å lage et åttende torg: Flytt de to øverste lilla brikkene inn i 2/3 høydeområdet (området innenfor 2/3 braketten): skygge rektanglene umiddelbart til høyre og umiddelbart over det lilla området:

Dette viser at det er 3 * 2, eller 6, lilla deler av 8 * 3 • eller 24, deler i det hele tatt. Det lilla området er lik 1/4, og det kom fra produktet av 2/3 multiplisert med hva? Vi kan se at den andre faktoren er 3/8.

Problem A3
en by planlegger å bygge et fellesskap hage som vil dekke 2/3 av en kvadratmil. De ønsker å plassere den på en beite av en gammel hest gård. En dimensjon av hagen området vil bli bestemt av et gjerde som er 3/4 av en mil lang. Bruk arealmodellen for divisjon for å bestemme den andre dimensjonen av det nye hageområdet.

Problem A4
Beskriv hvordan områdemodellen viser at kvotienten av to positive fraksjoner, hver mindre enn 1, må være større enn den første fraksjonen.

I Denne Delen: Fellesnevnermodellen For Divisjon
områdemodellen For deling av fraksjoner hjelper ikke å illustrere hvorfor algoritmen vi er mest kjent med (inverter divisoren og deretter multipliser) fungerer. Dessverre kan ingen modell vise det. Se Note 4 nedenfor.

Men her er en annen divisjonsalgoritme, en som vi kan forklare med en modell: Finn fellesnevneren, finn ekvivalente fraksjoner og del tellerne.

for å forstå modellen for denne algoritmen, la oss først gå tilbake til å gjennomgå noen av begrepene divisjon. Det er vanligvis lettere å beregne hvis du tenker på divisjon på en kvoterende måte. Dermed kan du si at 6 3 spør, » Hvor mange 3s er det i 6?»

deretter må vi forstå rollen som enheter i divisjon.

Problem A5
Hvilke, hvis noen, av disse spørsmålene gir et annet svar?
* Hvor mange 3 er det i 6?
* Hvor mange grupper på 3 tiere er det i 6 tiere?
* Hvor mange grupper av 3 femmere er det i 6 femmere?
* Hvor mange grupper på 3 tideler er det i 6 tideler?* Hvor mange grupper på 3 @s er det i 6 @s?

poenget her er at enhetene i problemet ikke betyr noe — hvis enhetene er samme enhet, forsvinner de når du deler.

dette bringer oss tilbake til den nye algoritmen for divisjon med fraksjoner: å dele to fraksjoner, finne en fellesnevner og deretter dele tellerne.

La oss prøve en visuell versjon av problemet vi gjorde før: 1/4 2/3. Finn først en fellesnevner:

1/4 2/3 = 3/12 8/12

deretter dele tellerne:

38 = 3/8

her er modellen for dette problemet, kalt fellesnevnermodellen:

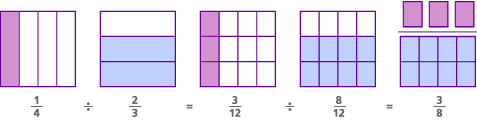
I dette problemet var det opprinnelige spørsmålet » Hvor mange 2 / 3 er det i 1/4 ?»Ved å finne en fellesnevner, endret vi spørsmålet til» Hvor mange 8/12s er det i 3/12?»- som er det samme som å spørre » Hvor mange 8s er det i 3?»Svaret på begge spørsmålene er det samme: «Det er 3/8 av en 8 i 3.»

Problem A6
Bruk fellesnevnermodellen til å dele 3/5 med 3/4.

Problem A7
Hvorfor har 0,6 0,2 det samme svaret som 6 2?

I Denne Delen: Oversette Prosessen Til Desimaler
du kan utvide det du har lært om operasjoner og brøker til desimaler også. Husk at et avsluttende desimal kan betraktes som en brøkdel med en kraft på 10 som nevner (f.eks. 0,4 = 4/10). Se Note 5 nedenfor.

Hvorfor trenger vi å stille opp desimalene når vi legger til eller trekker desimaler?
vi må stille opp desimaltallene fordi vi bare kan legge til eller trekke fra hvis enhetene er de samme. Ved å justere desimaltallene, sørger vi for at vi legger til eller trekker fra sifre som har samme stedverdier, akkurat som vi gjør når vi legger til eller trekker fra hele tall.

hvorfor teller vi desimaler når vi multipliserer desimaler?
Fra delen om eksponenter I Økt 3 vet vi at multiplikasjon med eksponenter krever å legge til eller» telle » eksponentene. Så for eksempel er 0,2 * 0,03 i eksponentiell form følgende:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

eksponentene er -1 og -2, som er henholdsvis ett og to steder til høyre for desimaltegnet. Produktet vil da ha en eksponent som er summen av -1 og -2 (dvs.-3), og er tre steder til høyre for desimaltegnet. Produktet av 0,2 * 0,03 er 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

Hvorfor flytter vi desimaltallene når vi deler med desimaler?
denne prosessen er relatert til å finne ekvivalente fraksjoner. Du kan tenke på divisjonen som en brøkdel. Siden problemet 2.5 0.05 er vanskelig å visualisere, skriv det som 2,5 / 0,05. Du trenger et helt tall i nevnen, så multipliser med 100 for å få et helt tall. For å kompensere for å multiplisere nevneren med 100, må du også multiplisere telleren med 100. Det betyr at du faktisk multipliseres med 100/100 eller 1, som ikke endrer verdien av brøkdelen. Slik ser prosessen ut: