Designer ‘ s Guide to isometrische projectie

de term “isometrisch” is een van de meest verkeerd gebruikte woorden in de ontwerpindustrie. We hebben de neiging om elke niet-perspectief 3-dimensionale tekening “isometrisch te noemen.”

een van de recente voorbeelden van pseudo-isometrische kunstwerken is het Old Medium logo, gebruikt van 2015 tot 2017 . Het is ontworpen op een parallel (axonometrisch) raster, maar het is helemaal niet isometrisch.

In dit artikel zal ik de verschillen tussen isometrische en andere soorten projecties toelichten.

picturale tekeningen

het kunnen visualiseren van driedimensionale vormen is een vaardigheid die elke ontwerper en ingenieur moet beheersen. Dit is vooral belangrijk in 3D-modellering. Er is echter een duidelijk verschil tussen het tekenen van een visie die eruit ziet als driedimensionaal en het creëren van een echt 3D-model.

echte 3D-modellen kunnen op het scherm worden gedraaid om vanuit elke hoek te worden bekeken. De computer berekent de punten, hoeken en oppervlakken van het object in de ruimte. Vervolgens wordt het resultaat op een flatscreen weergegeven als zogenaamde picturale tekeningen.

het woord pictorial betekent “zoals een afbeelding.”Het verwijst naar elke realistische vorm van tekening portretteren hoogte, breedte en diepte van een object. Picturale tekeningen zijn uiterst nuttig wanneer we ontwerpen moeten communiceren aan mensen die geen technische opleiding hebben in het interpreteren van multiview projecties.

verschillende vormen van picturale projecties worden gebruikt in ontwerp-en technische tekeningen:

• perspectief – meest realistische tekeningen. Onze ogen zien objecten in perspectief. Er zijn drie soorten perspectiefprojecties: een -, twee-en driepuntsperspectief.

• schuin-minst realistisch. Slechts één of twee zijden in schuine uitsteeksels hebben ware vorm en grootte. Er zijn drie soorten schuine projecties: cabinet, cavalier en general.

• axonometrische projecties zijn realistischer dan schuin. Horizontale randen van een object in axonometrische projecties zijn evenwijdig aan elkaar en schuin naar het vlak. Er zijn drie soorten axonometrische projecties: isometrisch, dimetrisch en trimetrisch.

axonometrische projecties

axonometrische projecties zijn de meest voorkomende manier om 3-dimensionale objecten weer te geven zonder perspectief. In tegenstelling tot perspectieftekeningen komen alle assen in axonometrische projecties niet samen en blijven ze altijd parallel.

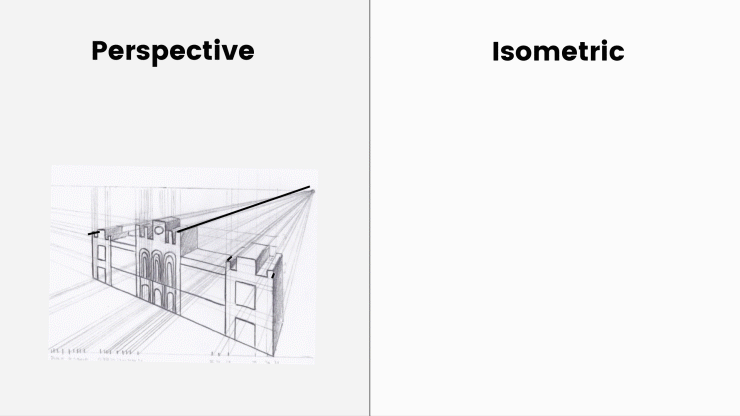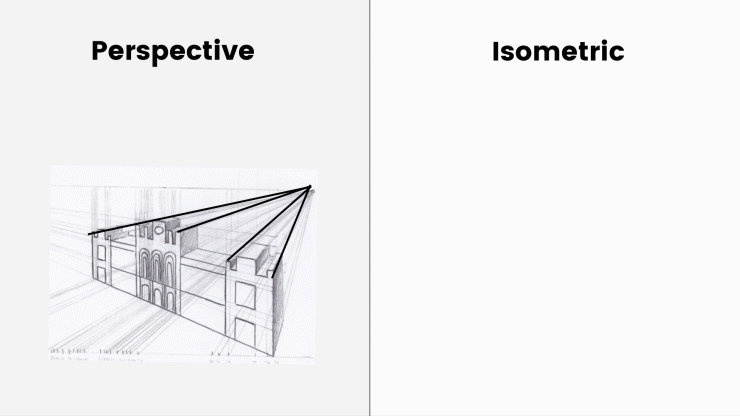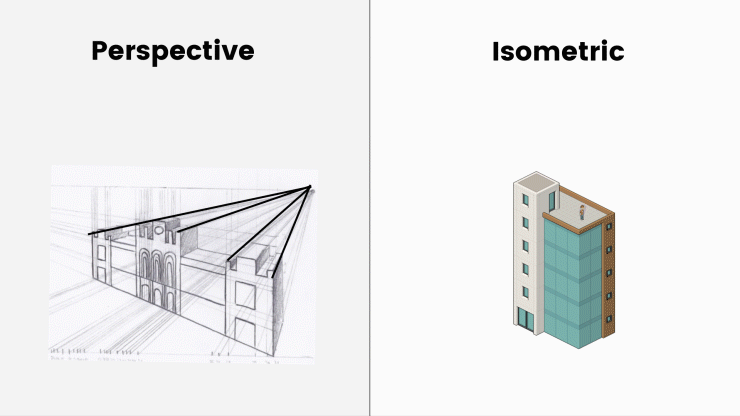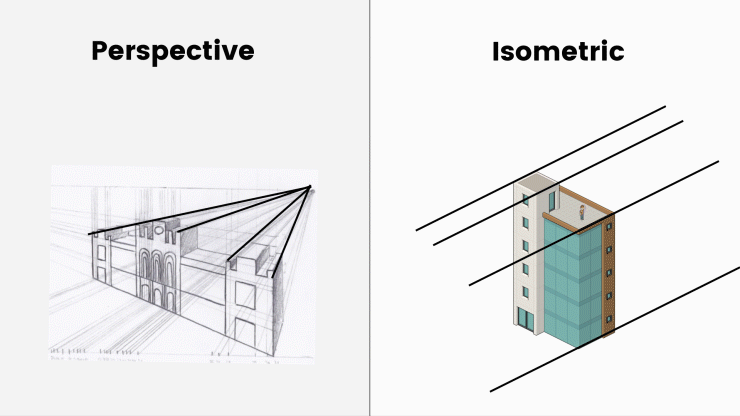
geen verdwijnpunten, geen horizonlijn. Het object wordt niet kleiner met afstand. Het was erg belangrijk voor de game-industrie tussen 1980 en 1990, omdat computers uit die tijd met beperkte middelen een object slechts één keer moeten maken.

het hoofddoel van axonometrische projecties is de vorm en de grootte van een object aan te geven. Ze zijn zo ontworpen dat je metingen kunt doen van een object uit deze projecties.

alle drie de typen axonometrische projecties zijn gebouwd op het raster waar de x-en Z-assen naar het horizontale vlak neigen. De Y-as blijft altijd loodrecht op het horizontale vlak staan.

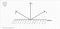
de hoek tussen de” horizontale ” X-en Z-assen en het horizontale vlak bepaalt het type axonometrische projectie.

isometrische projectie

isometrisch (wat “gelijke maat” betekent) is een type parallelle (axonometrische) projectie, waarbij de x-en Z-as schuin staan ten opzichte van het horizontale vlak onder een hoek van 30⁰. De hoek tussen axonometrische Assen is gelijk aan 120⁰.

een perfecte kubus in een isometrische projectie zou eruit zien als een perfecte zeshoek.

in Gravit Designer kunt u het ware isometrische raster direct uit de doos bouwen.

omdat alle randen van een isometrisch object onder dezelfde hoek hellend zijn, zijn ze even verkort. Hiermee kunt u metingen van elke kant van een object met behulp van dezelfde schaal.

de meeste ontwerpers negeren de verkorting tijdens de schetsfase en bouwen isometrische weergaven van een object met de werkelijke lengte. Het eindresultaat zou een isometrische schets zijn, geen projectie

isometrie bouwen zonder een raster

met behulp van een isometrisch raster is niet de enige manier om isometrische kunstwerken te tekenen in Gravit Designer.

ze kunnen worden geconstrueerd uit MultiView projecties (boven, voor, zij, enz.). De meest voorkomende en eenvoudige technieken zijn SR45⁰ en SSR30⁰.

dit zijn zeer handige methoden, wanneer u anisometrische mock-up van uw ontwerp met een paar klikken moet maken:

SR45⁰ techniek

“SR45⁰” staat voor schaal en roteren onder een hoek van 45⁰. De schaalverhouding is 0,577 of meer preciously tan (30⁰).

u kunt isometrische projecties maken via SR45⁰ met behulp van het transformatiepaneel van Gravit Designer in twee eenvoudige stappen

Stap 1: object roteren op 45⁰

Stap 2 : object schalen

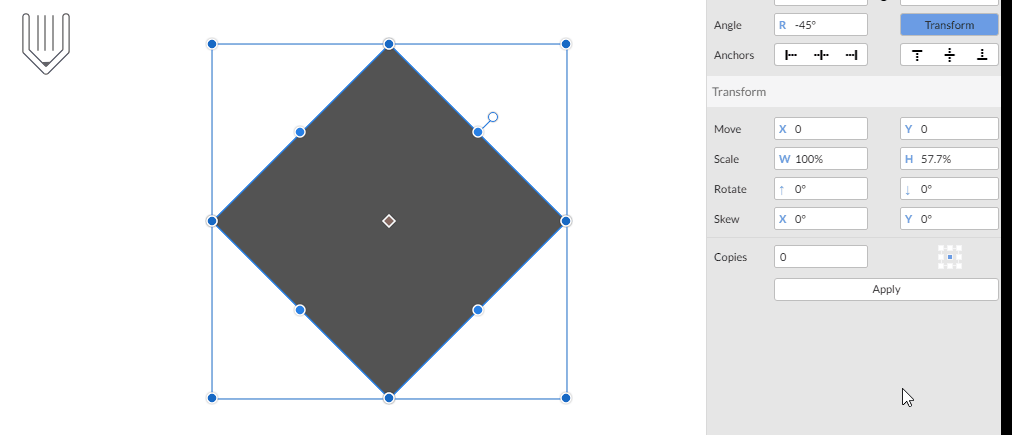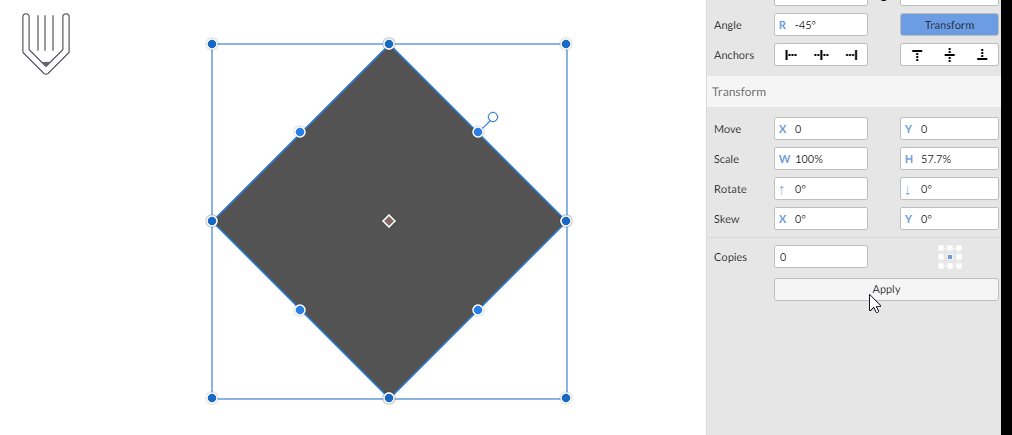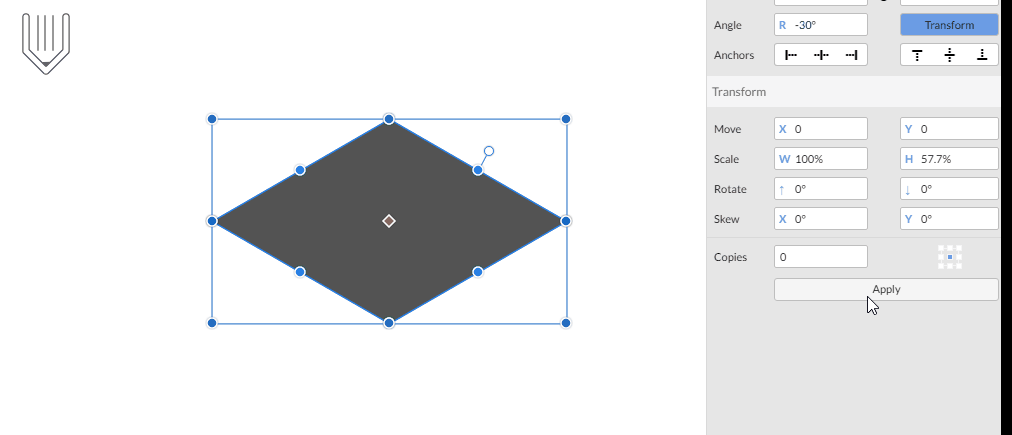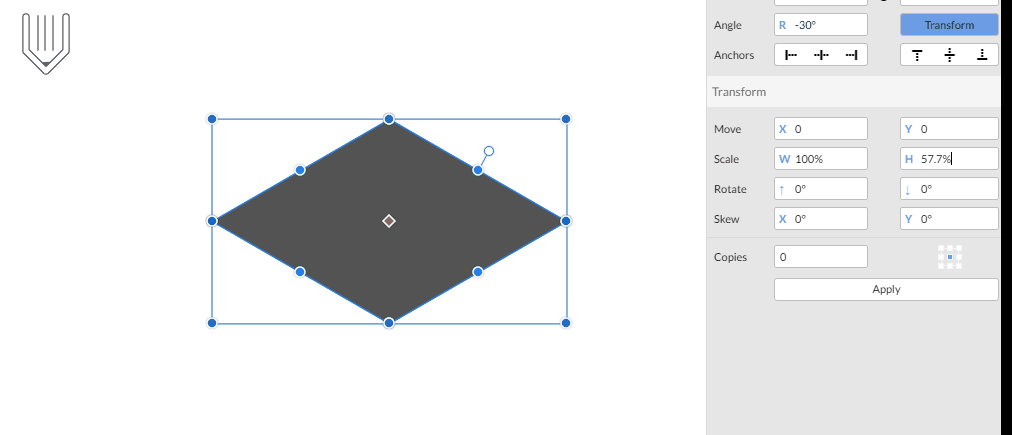
SSR30 technique techniek

“SSR30⁰” is een meer populaire en flexibele methode voor het maken van isometrische kunstwerken. Met SSR30⁰ kunt u snel boven, links en rechts isometrische weergaven maken.

SSR30⁰ staat voor schaal, schuin en roteren op 30⁰.

ontwerpen van andere axonometrische projecties met Gravit Designer

bij dimetrische projecties zijn slechts twee zijden even verkort. De x-en Z-assen staan nog steeds in dezelfde hoek ten opzichte van het horizontale vlak, maar niet op 30°. Hoeken tussen Assen zijn niet gelijk.

Trimetrische projecties

alle hoeken van een trimetrische projecties zijn verschillend, daarom zijn alle zijden (randen) en assen ongelijk verkort.

u kunt een breed scala aan hoeken gebruiken om trimetrische en dimetrische kunstwerken te bouwen, maar vermijd kleine. Naar mijn mening maakt het de projectie een tikkeltje te vlak:

anatomie van een Medium logo

het oorspronkelijke Medium logo is ontworpen op een niet-isometrisch raster, waar de x-en Y-as schuin staan ten opzichte van het horizontale vlak onder een hoek van respectievelijk-27⁰ en 60⁰. Dus, het Medium logo is gebouwd op trimetrische raster.

als je het tot nu toe hebt gehaald, gefeliciteerd! Ik hoop dat alle GIF ’s en jpg’ s niet geven uw browser (of zelfs u 😉) een overkill. Ik hoop ook dat je wat waarde voor jezelf en een aantal nieuwe tools om gebruik te maken in uw isometrische tekeningen.

Website | Facebook | Twitter / Forum