ułamki, procenty i proporcje część A: modele mnożenia i dzielenia ułamków (45 minut)

W tej części: Model obszaru mnożenia
w przeszłości można było nauczyć się poszczególnych algorytmów mnożenia i dzielenia ułamków. Użyjemy teraz niektórych modeli wizualnych, które wykorzystaliśmy wcześniej w tym kursie, aby lepiej zrozumieć, co tak naprawdę dzieje się podczas wykonywania tych operacji. Zob. Uwaga 2 poniżej.

najpierw użyjemy modelu obszaru-takiego, który nakłada kwadraty, które są podzielone na odpowiednią liczbę regionów i zacienione w razie potrzeby – aby wyjaśnić, co się dzieje, gdy mnożysz ułamki. Na przykład, oto jak użylibyśmy modelu obszaru do zademonstrowania problemu 3/8 • 2/3:

odcień jeden kwadrat, podzielony pionowo, aby reprezentować 3/8 (pokazane poniżej w kolorze różowym):		Cień inny kwadrat, podzielony poziomo, aby reprezentować 2/3 (pokazano poniżej na niebiesko):		nałożyć dwa kwadraty. Produkt jest obszarem podwójnie cieniowanym (pokazanym poniżej na fioletowo):

Jaka jest wartość tego fioletowego obszaru? Istnieje 3 * 2, lub 6, fioletowe części z 8 * 3, lub 24, części we wszystkich, więc wartość fioletowy obszar jest 6/24.

ten model wizualnie demonstruje znany algorytm: aby pomnożyć dwa ułamki, pomnożyć liczniki, a następnie pomnożyć mianowniki. Algorytm ten „zlicza” zarówno fioletowe części (iloczyn dwóch liczników), jak i całkowitą liczbę części (iloczyn dwóch mianowników).

możemy również użyć tego modelu do „zmniejszenia” frakcji. Najpierw zamieniamy pozycje niektórych fioletowych części. Dwie z fioletowych części można przesunąć na górę, a zatem dwie z ósemek są teraz zacienione. Te dwie ósme są tym samym obszarem co jedna czwarta:

W tej części: spróbuj sam
Stwórz własne kwadratowe przezroczystości, aby nałożyć je na siebie, i modeluj rozwiązanie dla każdego kroku w problemie A1 poniżej.

Problem A1
zdjęcie z lotu ptaka przedstawia wymiary trzech pól w ułamkach mili. Użyj modelu obszaru, którego dopiero się nauczyłeś, aby modelować obszar w milach kwadratowych każdego z tych pól:
a. 3/4 • 1/3
b. 3/5 • 2/3
c. 1/4 • 8/9

Problem A2
opisz, w jaki sposób model powierzchni pokazuje, że iloczyn dwóch dodatnich frakcji, z których każda jest mniejsza niż 1, musi być mniejszy niż jedna z frakcji.

Segment wideo
w tym segmencie Jeanne i Liz używają modelu obszaru do mnożenia ułamków. Odnoszą ten model do algorytmu mnożenia i sprawdzają sposoby wizualnej redukcji ułamków. Obejrzyj ten segment wideo po zakończeniu problemów A1 i A2.

ten fragment można znaleźć na filmie z sesji około 4 minut i 32 sekundy po logo Annenberg Media.

W tej części: Model obszaru dla dzielenia
możemy zastosować model obszaru dla mnożenia ułamków, aby zobrazować podział dwóch ułamków, gdy każdy jest mniejszy niż 1. Aby modelować dzielenie za pomocą ułamków, mniej więcej odwracamy proces używany do mnożenia. Zaczynamy od obszaru, którego szukamy i znajdujemy jeden z brakujących czynników tworzących ten obszar. Zob. Uwaga 3 poniżej.

na przykład, oto jak użyjemy modelu do zademonstrowania problemu 1/4 2/3:

Cień jeden kwadrat, podzielony pionowo, aby reprezentować 1/4 (jak w modelu mnożenia, jest cieniowany fioletowy):		nałożyć kwadrat podzielony na trzecie, umieszczony poziomo, na kwadrat czwartych i narysować wspornik na prawo od kwadratu trzeciego, aby pokazać rozmiar 2/3:

to, co teraz widzicie, to fioletowy (1/4) obszar i rozmiar jednego z czynników, które stworzyły ten obszar.

z modelu mnożenia wiemy, że iloczyn 2/3 i innego czynnika (ilorazu) definiuje pole o wielkości równej 1/4. Aby znaleźć iloraz, musimy przesunąć górną część fioletowego obszaru tak, aby miał taką samą wysokość jak współczynnik 2/3.

podziel kwadrat czwarty, aby uzyskać kwadrat ósmy:		Przesuń dwie górne fioletowe części w obszar wysokości 2/3 (obszar w obrębie wspornika 2/3):		teraz zasłoń prostokąty bezpośrednio w prawo i bezpośrednio nad Fioletowym obszarem:

to pokazuje, że są 3 • 2, lub 6, fioletowe części z 8 * 3, lub 24, części we wszystkich. Fioletowy obszar równa się 1/4, i pochodzi z iloczynu 2/3 pomnożonego przez co? Widzimy, że drugi czynnik to 3/8.

Problem A3
miasto planuje wybudować ogród komunalny, który obejmie 2/3 mili kwadratowej. Chcieliby go umiejscowić na pastwisku starej stadniny koni. Jeden wymiar powierzchni ogrodu zostanie określony przez ogrodzenie o długości 3/4 mili. Użyj modelu obszaru do podziału, aby określić inny wymiar nowego obszaru ogrodu.

Problem A4
opisz, w jaki sposób model obszaru pokazuje, że iloraz dwóch dodatnich ułamków, z których każda jest mniejsza niż 1, musi być większy niż pierwszy ułamek.

W Tej Części: Model wspólnego mianownika dla dzielenia
model obszaru dla dzielenia ułamków nie pomaga zilustrować, dlaczego algorytm, który znamy najlepiej (Odwróć dzielnik, a następnie pomnóż) działa. Niestety, żaden model nie może tego pokazać. Zob. Uwaga 4 poniżej.

ale tutaj jest inny algorytm dzielenia, który możemy wyjaśnić za pomocą modelu: znajdź wspólny mianownik, znajdź równoważne ułamki i podziel liczniki.

aby zrozumieć model tego algorytmu, wróćmy najpierw do przeglądu niektórych pojęć podziału. Zwykle łatwiej jest obliczyć, jeśli pomyśli się o podziale w sposób cytatowy. Można więc powiedzieć, że 6 3 pyta: „Ile jest 3 w 6?”

następnie musimy zrozumieć rolę jednostek w dywizji.

Problem A5
które z tych pytań daje inną odpowiedź?
ile jest 3 w 6?
* ile jest grup po 3 dziesiątki w 6 dziesiątkach?
ile jest grup po 3 piątki w 6 piątkach?
* ile jest grup 3 dziesiątych w 6 dziesiątych?* Ile jest grup 3 @s W 6 @s?
• ile jest grup po 3 anythings w 6 anythings (o ile oba anythings odnoszą się do tej samej jednostki)?

chodzi o to, że jednostki problemu nie mają znaczenia — jeśli jednostki są tą samą jednostką, znikają po podziale.

to sprowadza nas do nowego algorytmu dzielenia z ułamkami: aby podzielić dwa ułamki, znajdź wspólny mianownik, a następnie podziel liczniki.

spróbujmy wizualnej wersji problemu, który zrobiliśmy wcześniej: 1/4 2/3. Najpierw znajdź wspólny mianownik:

1/4 2/3 = 3/12 8/12

następnie podziel liczniki:

38 = 3/8

oto model tego problemu, zwany modelem wspólnego mianownika:

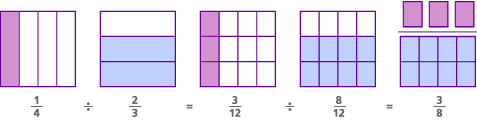
W tym problemie, w efekcie, oryginalne pytanie brzmiało ” ile 2 / 3s jest w 1/4?”Znajdując wspólny mianownik, zmieniliśmy pytanie na” ile jest 8/12 W 3/12?”- co jest tym samym, co pytanie ” Ile ósemek jest w 3?”Odpowiedź na oba pytania jest taka sama:” jest 3/8 z 8 W 3.”

Problem A6
użyj modelu wspólnego mianownika, aby podzielić 3/5 przez 3/4.

Problem A7
dlaczego 0.6 0.2 ma taką samą odpowiedź jak 6 2?

W tej części: tłumacząc Proces na ułamki dziesiętne
możesz rozszerzyć to, czego nauczyłeś się o operacjach i ułamkach, także na ułamki dziesiętne. Pamiętaj, że kończący się dziesiętny może być traktowany jako ułamek o potędze 10 jako mianownik (np. 0.4 = 4/10). Zob. Uwaga 5 poniżej.

dlaczego musimy wyrównać punkty dziesiętne, gdy dodajemy lub odejmujemy dziesiętne?
musimy wyrównać punkty dziesiętne, ponieważ możemy dodawać lub odejmować tylko wtedy, gdy jednostki są takie same. Wyrównując punkty dziesiętne, upewniamy się, że dodajemy lub odejmujemy cyfry, które mają te same wartości miejsca, tak jak robimy to, gdy dodajemy lub odejmujemy liczby całkowite.

dlaczego liczymy miejsca po przecinku, gdy mnożymy po przecinku?
z sekcji o wykładnikach w sesji 3 wiemy, że mnożenie przez wykładniki wymaga dodania lub „liczenia” wykładników. Tak więc, na przykład, 0.2 • 0.03 w formie wykładniczej jest następujący:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

wykładniki to -1 i -2, które są odpowiednio jednym i dwoma miejscami na prawo od przecinka dziesiętnego. Iloczyn będzie miał wykładnik, który jest sumą -1 i -2 (tj. -3) i jest trzy miejsca na prawo od przecinka dziesiętnego. Produkt 0,2 • 0,03 jest 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

dlaczego przesuwamy punkty dziesiętne dzieląc je przecinkami?
proces ten jest związany ze znalezieniem ułamków równoważnych . Możesz myśleć o podziale jako o ułamku. Od problemu 2.5 0.05 jest trudne do wizualizacji, napisz to jako 2.5/0.05. Potrzebujesz liczby całkowitej w mianowniku, więc pomnóż przez 100, aby otrzymać liczbę całkowitą. Aby zrekompensować pomnożenie mianownika przez 100, musisz również pomnożyć licznik przez 100. To znaczy, że faktycznie pomnożyliśmy przez 100/100, czyli 1, co nie zmienia wartości ułamka. Oto jak wygląda proces: