Frações, Porcentagens, Proporções e Parte A: Modelos para a Multiplicação e Divisão de Frações (45 minutos)

Nesta Parte: Área de Modelo para a Multiplicação de
No passado, você pode ter aprendido particular algoritmos para multiplicação e divisão de frações. Agora vamos usar alguns dos modelos visuais que empregamos anteriormente neste curso para entender melhor o que está realmente acontecendo quando realizamos essas operações. Ver Nota 2 infra.

primeiro vamos usar um modelo de área — um que sobrepõe quadrados que são particionados no número apropriado de regiões, e sombreados conforme necessário — para esclarecer o que acontece quando você multiplica frações. Por exemplo, aqui está como devemos utilizar o modelo de área para demonstrar o problema 3/8 • 2/3:

a Sombra de um quadrado, particionados verticalmente, para representar 3/8 (mostrado abaixo em cor-de-rosa):		a Sombra de outra praça, particionado horizontalmente, de forma a representar 2/3 (mostrado abaixo, em azul):		Sobrepor as duas praças. O produto é a área que é duplo-sombreadas (mostrado abaixo em roxo):

Qual é o valor desta área de roxo? Há 3 * 2, ou 6, partes roxas de 8 * 3, ou 24, partes em todos, de modo que o valor da área púrpura é 6/24.

este modelo demonstra visualmente o algoritmo familiar: multiplicar duas frações, multiplicar os numeradores e, em seguida, multiplicar os denominadores. Este algoritmo “conta” tanto as partes roxas (o produto dos dois numeradores) quanto o número total de partes (o produto dos dois denominadores).

também podemos usar este modelo para” reduzir ” a fracção. Primeiro trocamos as posições de algumas das partes roxas. Duas das partes roxas podem ser movidas para o topo, e assim, duas das oitavas são agora sombreadas. Estas duas oitavas são a mesma área que um quarto:

nesta parte: Tente você mesmo
Faça suas próprias transparências quadradas para sobrepor, e modele a solução para cada passo no problema A1 abaixo.

problema A1
uma foto aérea de terras agrícolas mostra as dimensões de três campos em frações de uma milha. Use a área de modelo que você acabou de aprender para modelar a área em quilômetros quadrados de cada um destes campos:
um. 3/4 • 1/3
b. 3/5 • 2/3
c. 1/4 • 8/9

Problema A2
Descrever como o modelo de área mostra que o produto de dois positiva frações, cada um com menos de 1, deve ser menor do que qualquer uma das frações.

segmento de vídeo
neste segmento, Jeanne e Liz usam o modelo de área para multiplicar frações. Eles relacionam este modelo com o algoritmo de multiplicação e verificam formas de reduzir visualmente frações. Assista a este segmento de vídeo depois de ter completado os problemas A1 e A2.

pode encontrar este segmento no vídeo da sessão aproximadamente 4 minutos e 32 segundos após o logótipo da mídia Annenberg.

Nesta Parte: Modelo de Área para a Divisão
podemos aplicar o modelo de área para a multiplicação de frações para visualizar a divisão de duas frações, quando cada um é menor que 1. Para modelar a divisão com frações, nós mais ou menos revertemos o processo usado para multiplicação. Começamos com uma área que estamos procurando, e encontramos um dos fatores faltantes que compõem essa área. Ver Nota 3 infra.

Por exemplo, aqui está como gostaria de usar o modelo para demonstrar o problema 1/4 2/3:

a Sombra de um quadrado, particionados verticalmente, para representar 1/4 (como na multiplicação do modelo, é sombreada roxo):		Sobrepor um quadrado dividido em terços, posicionado na horizontal, para os quartos quadrado, e desenhar um suporte para o direito dos terços praça para mostrar o tamanho de 2/3:

o Que você vê agora é o roxo (1/4) a área e o tamanho de um dos fatores que fez com que essa área.

sabemos a partir do modelo de multiplicação que o produto de 2/3 e outro fator (o quociente) define uma área equivalente em tamanho a 1/4. Para encontrar o quociente, precisamos mover a parte superior da área púrpura para que seja a mesma altura que o fator 2/3.

subdividir o quadragésimo quadrado para fazer um octogésimo quadrado:		Mover a parte superior dois roxo peças para a 2/3 da altura da área (a área dentro de 2/3 suporte):		Agora sombra retângulos imediatamente para a direita e imediatamente acima da área de roxo:

Isso mostra que há 3 • 2 ou 6, roxo peças 8 • 3 ou 24, em todas as partes. A área púrpura é igual a 1/4, e veio do produto de 2/3 multiplicado por quê? Podemos ver que o outro fator é 3/8.

problema A3
uma cidade planeja construir um jardim comunitário que cobrirá 2/3 de uma milha quadrada. Eles gostariam de colocá-lo num pasto de uma velha fazenda de cavalos. Uma dimensão da área do jardim será determinada por uma cerca de 3/4 de uma milha de comprimento. Use o modelo de área para a divisão para determinar a outra dimensão da nova área do jardim.

problema A4
descreva como o modelo de área mostra que o quociente de duas fracções positivas, cada uma inferior a 1, deve ser maior do que a primeira fracção.

Nesta Parte: O modelo de denominador comum para a divisão
o modelo de área para a divisão de frações não ajuda a ilustrar por que o algoritmo que estamos mais familiarizados com (inverter o divisor e, em seguida, multiplicar) funciona. Infelizmente, nenhum modelo pode mostrar isso. Ver Nota 4 infra.

mas aqui está um algoritmo de divisão diferente, um que podemos explicar com um modelo: encontrar o denominador comum, encontrar as frações equivalentes, e dividir os numeradores.

a fim de entender o modelo para este algoritmo, vamos primeiro voltar para rever alguns dos conceitos de divisão. É geralmente mais fácil de calcular se você pensar sobre a divisão de uma forma citativa. Assim, você pode dizer que 6 3 pergunta: “Quantos 3s existem em 6?Em seguida, precisamos entender o papel das unidades na divisão.O problema A5
que, se for caso disso, destas perguntas produz uma resposta diferente? * quantos grupos de 3 décimos existem em 6 décimos?•Quantos grupos de 3 @s existem em 6 @s?
* quantos grupos de 3 anythings existem em 6 anythings (desde que ambos os anythings se referem à mesma unidade)?

o ponto aqui é que as unidades do problema não importam — se as unidades são a mesma entidade, elas desaparecem quando você divide.

isto traz-nos de volta ao novo algoritmo para a divisão com fracções: para dividir duas fracções, encontrar um denominador comum e, em seguida, dividir os numeradores.Vamos tentar uma versão visual do problema que fizemos antes: 1/4 2/3. Primeiro, encontrar um denominador comum:

1/4 2/3 = 3/12 8/12

em seguida, dividir os numeradores:

38 = 3/8

Aqui é o modelo para este problema, chamado de denominador comum do modelo:

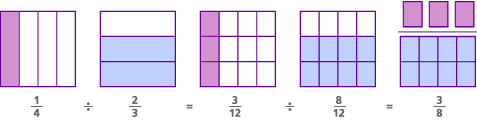
neste problema, na verdade, a pergunta original era “quantos 2/3s existem em 1/4?”Ao encontrar um denominador comum, nós mudamos a pergunta para” quantos 8 / 12s existem em 3/12?”—que é o mesmo que perguntar ” quantos 8 são em 3?”A resposta a ambas as perguntas é a mesma:” há 3/8 de um 8 em 3.”

problema A6
utilizar o modelo do denominador comum para dividir 3/5 por 3/4.

problema A7
por que razão 0,6 0.2 tem a mesma resposta que 6 2?

nesta parte: traduzindo o processo para decimais
você pode estender o que você aprendeu sobre Operações e frações para decimais também. Lembre-se que uma decimal terminal pode ser considerada como uma fração com uma potência de 10 como o denominador (por exemplo, 0.4 = 4/10). Ver Nota 5 infra.

por que precisamos de alinhar os pontos decimais quando adicionamos ou subtraímos decimais?
precisamos alinhar os pontos decimais porque só podemos adicionar ou subtrair se as unidades forem as mesmas. Alinhando os pontos decimais, certificamo-nos de que estamos a adicionar ou subtrair dígitos que têm os mesmos valores de lugar, tal como fazemos quando adicionamos ou subtraímos números inteiros.Por que contamos as casas decimais quando multiplicamos as casas decimais?
da seção sobre expoentes na sessão 3, sabemos que a multiplicação com expoentes requer a adição, ou “contagem”, dos expoentes. Assim, por exemplo, 0.2 • 0.03 na forma exponencial é o seguinte::

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

Os expoentes são -1 e -2, que são um e dois lugares, respectivamente, à direita do ponto decimal. O produto terá então um expoente que é a soma de -1 e -2 (isto é, -3), e é três lugares à direita do ponto decimal. O produto de 0,2 • 0.03 é 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

Por que mover os pontos decimais ao dividir com casas decimais?
este processo está relacionado a encontrar frações equivalentes. Podes pensar na divisão como uma fracção. Desde o problema 2.5 0.05 é difícil de visualizar, escrevê-lo como 2.5/0.05. Você precisa de um número inteiro no denominador, então multiplique por 100 para obter um número inteiro. Para compensar a multiplicação do denominador por 100, Você também deve multiplicar o numerador por 100. Isso significa que você realmente multiplicou por 100/100, ou 1, o que não altera o valor da fração. Aqui está como o processo se parece: