fracții, procente și rapoarte partea a: Modele pentru înmulțirea și împărțirea fracțiilor (45 minute)

în această parte: Model de zonă pentru înmulțire
în trecut, este posibil să fi învățat algoritmi specifici pentru înmulțirea și împărțirea fracțiilor. Acum vom folosi unele dintre modelele vizuale pe care le-am folosit mai devreme în acest curs pentru a înțelege mai bine ce se întâmplă de fapt atunci când efectuăm aceste operații. A se vedea nota 2 de mai jos.

mai întâi vom folosi un model de zonă — unul care suprapune pătrate care sunt partiționate în numărul corespunzător de regiuni și umbrite după cum este necesar — pentru a clarifica ce se întâmplă atunci când înmulțiți fracțiile. De exemplu, iată cum am folosi modelul de zonă pentru a demonstra problema 3/8 • 2/3:

umbrați un pătrat, împărțit vertical, pentru a reprezenta 3/8 (prezentat mai jos în roz):		umbriți un alt pătrat, împărțit orizontal, pentru a reprezenta 2/3 (prezentat mai jos în albastru):		suprapuneți cele două pătrate. Produsul este zona care este umbrită dublu (prezentată mai jos în violet):

care este valoarea acestei zone violet? Există 3 • 2, sau 6, părți violet din 8 • 3, sau 24, părți în toate, astfel încât valoarea zonei violet este de 6/24.

acest model demonstrează vizual algoritmul familiar: pentru a înmulți două fracții, înmulțiți numeratorii și apoi înmulțiți numitorii. Acest algoritm „numără” atât părțile purpurii (produsul celor doi numărători), cât și numărul total de părți (produsul celor doi numitori).

de asemenea, putem folosi acest model pentru a „reduce” fracția. Mai întâi schimbăm pozițiile unor părți purpurii. Două dintre părțile purpurii pot fi mutate în partea de sus și, astfel, două dintre optimi sunt acum umbrite. Aceste două optimi sunt aceeași zonă ca un sfert:

în această parte: încercați singur
Creați-vă propriile transparențe pătrate pentru a suprapune și modelați soluția pentru fiecare pas din problema a1 de mai jos.

problema A1
o fotografie aeriană a terenurilor agricole arată dimensiunile a trei câmpuri în fracțiuni de milă. Utilizați modelul de zonă pe care tocmai l-ați învățat să modelați zona în mile pătrate din fiecare dintre aceste câmpuri:
a. 3/4 • 1/3
b. 3/5 * 2/3
c. 1/4 • 8/9

problema A2
descrie modul în care modelul zonei arată că produsul a două fracții pozitive, fiecare mai mică de 1, trebuie să fie mai mică decât oricare dintre fracții.

Segment Video
în acest segment, Jeanne și Liz folosesc modelul de zonă pentru a multiplica fracțiile. Acestea raportează acest model la algoritmul de multiplicare și verifică modalitățile de reducere vizuală a fracțiilor. Urmăriți acest segment video după ce ați finalizat problemele A1 și A2.

puteți găsi acest segment pe videoclipul sesiunii la aproximativ 4 minute și 32 de secunde după sigla Media Annenberg.

în această parte: Model de zonă pentru divizare
putem aplica modelul de zonă pentru înmulțirea fracțiilor pentru a vizualiza împărțirea a două fracții atunci când fiecare este mai mică de 1. Pentru a modela diviziunea cu fracții, inversăm mai mult sau mai puțin procesul utilizat pentru multiplicare. Începem cu o zonă pe care o căutăm și găsim unul dintre factorii care lipsesc din acea zonă. A se vedea nota 3 de mai jos.

de exemplu, iată cum am folosi modelul pentru a demonstra problema 1/4 2/3:

umbrați un pătrat, împărțit vertical, pentru a reprezenta 1/4 (ca în modelul de multiplicare, este umbrit violet):		suprapuneți un pătrat împărțit în treimi, poziționat orizontal, pe pătratul pătratului și trageți un suport în dreapta pătratului treimilor pentru a arăta dimensiunea de 2/3:

ceea ce vedeți acum este zona purpurie (1/4) și dimensiunea unuia dintre factorii care au făcut acea zonă.

știm din modelul de multiplicare că produsul dintre 2/3 și un alt factor (coeficientul) definește o zonă echivalentă ca mărime cu 1/4. Pentru a găsi coeficientul, trebuie să mutăm partea superioară a zonei purpurii, astfel încât să aibă aceeași înălțime cu factorul 2/3.

subdivizați pătratul al patrulea pentru a face un pătrat al optulea:		mutați primele două piese violet în zona de înălțime 2/3 (zona din cadrul suportului 2/3):		acum umbrați dreptunghiurile imediat spre dreapta și imediat deasupra zonei violete:

acest lucru arată că există 3 • 2, sau 6, părți violet din 8 * 3, sau 24, părți în toate. Zona purpurie este egală cu 1/4 și provine din produsul de 2/3 înmulțit cu ce? Putem vedea că celălalt factor este 3/8.

problema A3
un oraș intenționează să construiască o grădină comunitară care să acopere 2/3 dintr-o milă pătrată. Ei ar dori să-l situeze pe o pășune a unei ferme de cai vechi. O dimensiune a zonei de grădină va fi determinată de un gard care are o lungime de 3/4 de mile. Utilizați modelul de zonă pentru divizare pentru a determina cealaltă dimensiune a noii zone de grădină.

problema A4
descrie modul în care modelul zonei arată că coeficientul a două fracții pozitive, fiecare mai mică de 1, trebuie să fie mai mare decât prima fracție.

În Această Parte: Modelul numitorului comun pentru diviziunea
modelul ariei pentru divizarea fracțiilor nu ajută la ilustrarea motivului pentru care algoritmul cu care suntem cel mai familiarizați (inversați divizorul și apoi înmulțiți) funcționează. Din păcate, niciun model nu poate arăta asta. A se vedea nota 4 de mai jos.

dar aici este un algoritm de diviziune diferit, unul pe care îl putem explica cu un model: Găsiți numitorul comun, găsiți fracțiile echivalente și împărțiți numărătorii.

pentru a înțelege modelul pentru acest algoritm, să ne întoarcem mai întâi pentru a revizui unele dintre conceptele de diviziune. De obicei, este mai ușor să calculați dacă vă gândiți la diviziune într-un mod cotativ. Astfel, puteți spune că 6 3 întreabă: „câte 3 sunt în 6?”

în continuare, trebuie să înțelegem rolul unităților în diviziune.

problema A5
care, dacă există, dintre aceste întrebări dă un răspuns diferit? • câte grupuri de 3 zeci există în 6 zeci?
• câte grupuri de 3 cinciari există în 6 cinciari?
• câte grupuri de 3 zecimi există în 6 zecimi?* Câte grupuri de 3 @s există în 6 @s?
• câte grupuri de 3 anythings sunt acolo în 6 anythings (atâta timp cât ambele anythings se referă la aceeași unitate)?

ideea este că unitățile problemei nu contează — dacă unitățile sunt aceeași entitate, ele dispar atunci când împărțiți.

acest lucru ne aduce înapoi la noul algoritm pentru împărțirea cu fracții: pentru a împărți două fracții, găsiți un numitor comun și apoi împărțiți numeratorii.

să încercăm o versiune vizuală a problemei pe care am făcut-o înainte: 1/4 2/3. Mai întâi, găsiți un numitor comun:

1/4 2/3 = 3/12 8/12

apoi, împărțiți numeratorii:

38 = 3/8

iată modelul pentru această problemă, numit modelul numitorului comun:

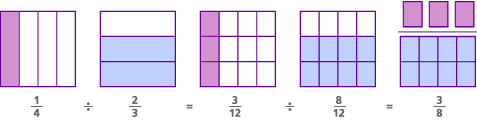
în această problemă, de fapt, întrebarea inițială a fost „câte 2 / 3 există în 1/4?”Prin găsirea unui numitor comun, am schimbat întrebarea în” câte 8 / 12 există în 3/12?— – care este același lucru cu întrebarea ” câte 8 sunt în 3?”Răspunsul la ambele întrebări este același: „există 3/8 dintr-un 8 din 3.”

problema A6
utilizați modelul numitor comun pentru a împărți 3/5 la 3/4.

problema A7
de ce 0.6 0.2 are același răspuns ca 6 2?

în această parte: traducerea procesului în zecimale
puteți extinde ceea ce ați învățat despre operații și fracții și la zecimale. Amintiți-vă că o zecimală terminală poate fi considerată ca o fracție cu o putere de 10 ca numitor (de exemplu, 0,4 = 4/10). A se vedea nota 5 de mai jos.

de ce trebuie să aliniem punctele zecimale atunci când adăugăm sau scădem zecimale?
trebuie să aliniem punctele zecimale, deoarece putem adăuga sau scădea numai dacă unitățile sunt aceleași. Prin alinierea punctelor zecimale, ne asigurăm că adăugăm sau scădem cifre care au aceleași valori de loc, la fel cum facem atunci când adăugăm sau scădem numere întregi.

de ce numărăm zecimalele când înmulțim zecimalele?
din secțiunea Despre exponenți din Sesiunea 3, știm că înmulțirea cu exponenți necesită adăugarea sau” numărarea ” exponenților. Deci, de exemplu, 0,2 * 0,03 în forma exponențială este următoarea:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

exponenții sunt -1 și -2, care sunt unul și respectiv două locuri, în dreapta punctului zecimal. Produsul va avea apoi un exponent care este suma -1 și -2 (adică -3) și este de trei locuri în dreapta punctului zecimal. Produsul 0.2 * 0.03 este 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

de ce mutăm punctele zecimale atunci când împărțim cu zecimale?
acest proces este legat de găsirea fracțiilor echivalente. Vă puteți gândi la diviziune ca la o fracțiune. Deoarece problema 2.5 0.05 este greu de vizualizat, scrie-l ca 2.5/0.05. Aveți nevoie de un număr întreg în numitor, deci înmulțiți cu 100 pentru a obține un număr întreg. Pentru a compensa înmulțirea numitorului cu 100, trebuie să înmulțiți și numărătorul cu 100. Asta înseamnă că de fapt înmulțit cu 100/100, sau 1, care nu se schimba valoarea fracției. Iată cum arată procesul: