fraktioner, procent och förhållanden Del a: modeller för multiplikation och delning av fraktioner (45 minuter)

BY admin
|

i den här delen: områdesmodell för multiplikation
tidigare kanske du har lärt dig särskilda algoritmer för multiplikation och delning av fraktioner. Vi kommer nu att använda några av de visuella modeller vi har använt tidigare i kursen för att bättre förstå vad som faktiskt händer när vi utför dessa operationer. Se anmärkning 2 nedan.

först använder vi en områdesmodell — en som överlagrar rutor som är uppdelade i lämpligt antal regioner och skuggade efter behov — för att klargöra vad som händer när du multiplicerar fraktioner. Här är till exempel hur vi skulle använda områdesmodellen för att visa problemet 3/8 • 2/3:

skugga en kvadrat, partitionerad vertikalt, för att representera 3/8 (visas nedan i rosa): skugga en annan kvadrat, uppdelad horisontellt, för att representera 2/3 (visas nedan i blått): lägg över de två rutorna. Produkten är det område som är dubbelskuggat (visas nedan i lila):

Vad är värdet av detta lila område? Det finns 3 • 2 eller 6, Lila delar av 8 * 3 eller 24, delar i alla, så värdet på det lila området är 6/24.

denna modell visar visuellt den välbekanta algoritmen: för att multiplicera två fraktioner, multiplicera täljarna och multiplicera sedan nämnarna. Denna algoritm ”räknar” både de lila delarna (produkten av de två täljarna) och det totala antalet delar (produkten av de två nämnarna).

vi kan också använda denna modell för att ”minska” fraktionen. Först byter vi positionerna för några av de lila delarna. Två av de lila delarna kan flyttas till toppen, och därmed är två av åttondelarna nu skuggade. Dessa två åttondelar är samma område som en fjärdedel:

i den här delen: prova själv
gör dina egna fyrkantiga OH-film för att överlappa, och modellera lösningen för varje steg i Problem A1 nedan.

Problem A1
ett flygfoto av jordbruksmark visar måtten på tre fält i fraktioner av en mil. Använd den områdesmodell du just har lärt dig att modellera området i kvadrat miles av vart och ett av dessa fält:
a. 3/4 * 1/3
b. 3/5 * 2/3
c. 1/4 • 8/9

Problem A2
Beskriv hur områdesmodellen visar att produkten av två positiva fraktioner, vardera mindre än 1, måste vara mindre än någon av fraktionerna.

videosegment
i detta segment använder Jeanne och Liz områdesmodellen för att multiplicera fraktioner. De relaterar denna modell till multiplikationsalgoritmen och kontrollerar sätt att visuellt minska fraktioner. Titta på det här videosegmentet när du har slutfört problemen A1 och A2.

du hittar det här segmentet på sessionsvideoen ungefär 4 minuter och 32 sekunder efter Annenberg Media-logotypen.

i denna del: områdesmodell för Division
vi kan tillämpa områdesmodellen för multiplikation av fraktioner för att visualisera uppdelningen av två fraktioner när var och en är mindre än 1. För att modellera division med fraktioner vänder vi mer eller mindre processen som används för multiplikation. Vi börjar med ett område vi letar efter, och vi hittar en av de saknade faktorerna som utgör det området. Se anmärkning 3 nedan.

till exempel, här är hur vi skulle använda modellen för att visa problemet 1/4 2/3:

skugga en kvadrat, partitionerad vertikalt, för att representera 1/4 (som i multiplikationsmodellen är den skuggad lila): överlagra en kvadrat uppdelad i tredjedelar, placerad horisontellt, på fjärde kvadraten och dra en konsol till höger om tredje kvadraten för att visa storleken på 2/3:

vad du ser nu är det lila (1/4) området och storleken på en av de faktorer som gjorde det området.

vi vet från multiplikationsmodellen att produkten av 2/3 och en annan faktor (kvoten) definierar ett område som motsvarar 1/4. För att hitta kvoten måste vi flytta den övre delen av det lila området så att det är samma höjd som 2/3-faktorn.

dela upp fjärde torget för att göra en åttonde kvadrat: flytta de två översta lila bitarna till 2/3 höjdområdet (området inom 2/3-fästet): skugga nu rektanglarna omedelbart till höger och omedelbart ovanför det lila området:

Detta visar att det finns 3 • 2, eller 6, Lila delar av 8 • 3, eller 24, delar i alla. Det lila området är lika med 1/4, och det kom från produkten av 2/3 multiplicerat med vad? Vi kan se att den andra faktorn är 3/8.

Problem A3
en stad planerar att bygga en gemensam trädgård som kommer att täcka 2/3 av en kvadratkilometer. De skulle vilja placera den på en betesmark på en gammal hästgård. En dimension av trädgårdsområdet kommer att bestämmas av ett staket som är 3/4 av en mil lång. Använd områdesmodellen för uppdelning för att bestämma den andra dimensionen i det nya trädgårdsområdet.

Problem A4
Beskriv hur områdesmodellen visar att kvoten för två positiva fraktioner, vardera mindre än 1, måste vara större än den första fraktionen.

I Denna Del: Den gemensamma Nämnarmodellen för Division
områdesmodellen för uppdelning av fraktioner hjälper inte till att illustrera varför algoritmen vi är mest bekanta med (invertera divisorn och sedan multiplicera) fungerar. Tyvärr kan ingen modell visa det. Se anmärkning 4 nedan.

men här är en annan divisionsalgoritm, en som vi kan förklara med en modell: hitta den gemensamma nämnaren, hitta motsvarande fraktioner och dela upp täljarna.

för att förstå modellen för denna algoritm, låt oss först gå tillbaka för att granska några av begreppen division. Det är vanligtvis lättare att beräkna om du tänker på division på ett quotativt sätt. Således kan du säga att 6 3 frågar, ” hur många 3s finns det i 6?”

Därefter måste vi förstå enheternas roll i divisionen.

Problem A5
vilka, om några, av dessa frågor ger ett annat svar?

poängen här är att enheterna i problemet inte spelar någon roll — om enheterna är samma enhet försvinner de när du delar upp.

detta leder oss tillbaka till den nya algoritmen för division med fraktioner: att dela två fraktioner, hitta en gemensam nämnare och sedan dela täljarna.

Låt oss prova en visuell version av problemet vi gjorde tidigare: 1/4 2/3. Först, hitta en gemensam nämnare:

1/4 2/3 = 3/12 8/12

därefter dela upp täljarna:

38 = 3/8

här är modellen för detta problem, kallad den gemensamma nämnaren modell:

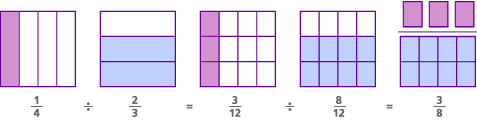
i detta problem var i själva verket den ursprungliga frågan ” hur många 2/3s finns det i 1/4?”Genom att hitta en gemensam nämnare ändrade vi frågan till” hur många 8 / 12s finns det i 3/12?”- vilket är detsamma som att fråga ” hur många 8s finns det i 3?”Svaret på båda frågorna är detsamma:” Det finns 3/8 av en 8 i 3.”

Problem A6
använd den gemensamma nämnaren för att dela 3/5 med 3/4.

Problem A7
Varför har 0.6 0.2 samma svar som 6 2?

i den här delen: översätta processen till decimaler
du kan utöka vad du har lärt dig om operationer och bråk till decimaler också. Kom ihåg att en avslutande decimal kan betraktas som en bråkdel med en effekt på 10 som nämnare (t.ex. 0,4 = 4/10). Se anmärkning 5 nedan.

Varför behöver vi rada upp decimalerna när vi lägger till eller subtraherar decimaler?
vi måste rada upp decimalpunkterna eftersom vi bara kan lägga till eller subtrahera om enheterna är desamma. Genom att anpassa decimalpunkterna ser vi till att vi lägger till eller subtraherar siffror som har samma platsvärden, precis som vi gör när vi lägger till eller subtraherar heltal.

varför räknar vi decimalerna när vi multiplicerar decimaler?
från avsnittet om exponenter i Session 3 vet vi att multiplikation med exponenter kräver att man lägger till eller ”räknar” exponenterna. Så, till exempel, 0,2 • 0,03 i exponentiell form är följande:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

exponenterna är -1 och -2, som är en respektive två platser till höger om decimalpunkten. Produkten kommer då att ha en exponent som är summan av -1 och -2 (dvs -3) och är tre platser till höger om decimalpunkten. Produkten av 0,2 * 0,03 är 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

varför flyttar vi decimalerna när vi delar med decimaler?
denna process är relaterad till att hitta ekvivalenta fraktioner. Du kan tänka på uppdelningen som en bråkdel. Eftersom problemet 2.5 0.05 är svårt att visualisera, skriv det som 2.5 / 0.05. Du behöver ett heltal i nämnaren, så multiplicera med 100 för att få ett heltal. För att kompensera för att multiplicera nämnaren med 100 måste du också multiplicera täljaren med 100. Det betyder att du faktiskt multiplicerat med 100/100 eller 1, vilket inte ändrar värdet på fraktionen. Så här ser processen ut: