fraktioner, procentdele og forhold del A: modeller til multiplikation og opdeling af fraktioner (45 minutter)

BY admin
|

i denne del: områdemodel til multiplikation
tidligere har du muligvis lært bestemte algoritmer til multiplikation og opdeling af fraktioner. Vi vil nu bruge nogle af de visuelle modeller, vi har brugt tidligere på dette kursus for bedre at forstå, hvad der faktisk sker, når vi udfører disse operationer. Se Note 2 nedenfor.

først bruger vi en områdemodel — en, der overlejrer firkanter, der er opdelt i det passende antal regioner og skraveret efter behov — for at afklare, hvad der sker, når du multiplicerer brøker. Sådan bruger vi områdemodellen til at demonstrere problemet 3/8 • 2/3:

skygge en firkant, opdelt lodret, for at repræsentere 3/8 (vist nedenfor i pink): skygge en anden firkant, opdelt vandret, for at repræsentere 2/3 (vist nedenfor i blåt): overlejre de to firkanter. Produktet er det område, der er dobbeltskygget (vist nedenfor i lilla):

Hvad er værdien af dette lilla område? Der er 3 • 2 eller 6 Lilla dele ud af 8 • 3 eller 24 dele i alt, så værdien af det lilla område er 6/24.

denne model demonstrerer visuelt den velkendte algoritme: at multiplicere to fraktioner, multiplicere tællerne og derefter multiplicere nævnerne. Denne algoritme “tæller” både de lilla dele (produktet fra de to tællere) og det samlede antal dele (produktet fra de to nævnere).

vi kan også bruge denne model til at “reducere” fraktionen. Først bytter vi positionerne for nogle af de lilla dele. To af de lilla dele kan flyttes til toppen, og dermed er to af ottendedele nu skyggefulde. Disse to ottendedele er det samme område som en fjerdedel:

i denne del: prøv det selv
Lav dine egne firkantede transparenter til at overlejre, og model løsningen for hvert trin i Problem A1 nedenfor.

Problem A1
et luftfoto af landbrugsjord viser dimensionerne på tre felter i brøkdele af en kilometer. Brug den områdemodel, du lige har lært, til at modellere området i kvadrat miles af hvert af disse felter:
a. 3/4 * 1/3
b. 3/5 * 2/3
c. 1/4 • 8/9

Problem A2
Beskriv, hvordan arealmodellen viser, at produktet af to positive fraktioner, hver mindre end 1, skal være mindre end en af fraktionerne.

videosegment
i dette segment bruger Jeanne og Lise arealmodellen til at multiplicere fraktioner. De relaterer denne model til multiplikationsalgoritmen og kontrollerer måder at visuelt reducere fraktioner på. Se dette videosegment, når du har afsluttet problemer A1 og A2.

du kan finde dette segment på sessionsvideoen cirka 4 minutter og 32 sekunder efter Annenberg Media-logoet.

i denne del: områdemodel for Division
vi kan anvende områdemodellen til multiplikation af fraktioner for at visualisere opdelingen af to fraktioner, når hver er mindre end 1. For at modellere division med fraktioner vender vi mere eller mindre den proces, der anvendes til multiplikation. Vi starter med et område, vi leder efter, og vi finder en af de manglende faktorer, der udgør dette område. Se Note 3 nedenfor.

for eksempel, her er hvordan vi ville bruge modellen til at demonstrere problemet 1/4 2/3:

skygge en firkant, opdelt lodret, for at repræsentere 1/4 (som i multiplikationsmodellen er den skyggefuld lilla): overlejre en firkant opdelt i tredjedele, placeret vandret, på den fjerde firkant, og træk en beslag til højre for tredjedels firkant for at vise størrelsen på 2/3:

hvad du ser nu er det lilla (1/4) område og størrelsen af en af de faktorer, der gjorde dette område.

vi ved fra multiplikationsmodellen, at produktet af 2/3 og en anden faktor (kvotienten) definerer et areal svarende til 1/4. For at finde kvotienten skal vi flytte den øverste del af det lilla område, så det er den samme højde som 2/3 faktoren.

opdel den fjerde firkant for at lave en ottendedel firkant: Flyt de to øverste lilla stykker ind i 2/3 højdeområdet (området inden for 2/3 beslaget): nu skygge rektanglerne straks til højre og umiddelbart over det lilla område:

Dette viser, at der er 3 • 2 eller 6 Lilla dele ud af 8 • 3 eller 24 dele i alt. Det lilla område er lig med 1/4, og det kom fra produktet af 2/3 ganget med hvad? Vi kan se, at den anden faktor er 3/8.

Problem A3
en by planlægger at bygge en fælles have, der dækker 2/3 af en kvadratkilometer. De vil gerne placere det på en græs af en gammel hest gård. En dimension af haven området vil blive bestemt af et hegn, der er 3/4 af en mile lang. Brug arealmodellen til opdeling til at bestemme den anden dimension af det nye haveområde.

Problem A4
Beskriv, hvordan arealmodellen viser, at kvotienten af to positive fraktioner, hver mindre end 1, skal være større end den første fraktion.

I Denne Del: Fællesnævnermodellen for Division
områdemodellen for opdeling af fraktioner hjælper ikke med at illustrere, hvorfor den algoritme, vi er mest fortrolige med (inverter divisoren og multiplicer derefter) fungerer. Desværre kan ingen model vise det. Se Note 4 nedenfor.

men her er en anden divisionsalgoritme, en som vi kan forklare med en model: Find fællesnævneren, find de tilsvarende fraktioner og divider tællerne.

for at forstå modellen for denne algoritme, lad os først gå tilbage for at gennemgå nogle af begreberne division. Det er normalt lettere at beregne, hvis du tænker på opdeling på en citativ måde. Således kan du sige, at 6 3 spørger: “hvor mange 3′ er er der i 6?”

Dernæst skal vi forstå enhedernes rolle i division.

Problem A5
hvilket af disse spørgsmål giver et andet svar?
* hvor mange 3 ‘ er er der i 6?
* hvor mange grupper på 3 tiere er der i 6 tiere?
* hvor mange grupper af 3 fives er der i 6 fives?

pointen her er, at enhederne i problemet ikke betyder noget — hvis enhederne er den samme enhed, forsvinder de, når du deler.

dette bringer os tilbage til den nye algoritme til opdeling med brøker: at opdele to brøker, finde en fællesnævner og derefter opdele tællerne.

lad os prøve en visuel version af det problem, vi gjorde før: 1/4 2/3. Find først en fællesnævner:

1/4 2/3 = 3/12 8/12

derefter opdele tællerne:

38 = 3/8

her er modellen til dette problem, kaldet fællesnævnermodellen:

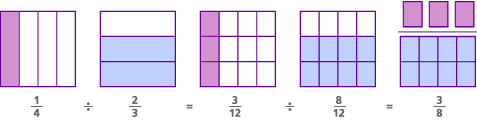
i dette problem var det oprindelige spørgsmål faktisk “hvor mange 2/3′ er er der i 1/4?”Ved at finde en fællesnævner ændrede vi spørgsmålet til” hvor mange 8/12 ‘ er er der i 3/12?”- hvilket er det samme som at spørge “Hvor mange 8’ er er der i 3?”Svaret på begge spørgsmål er det samme:” der er 3/8 af en 8 i 3.”

Problem A6
brug fællesnævnermodellen til at opdele 3/5 med 3/4.

Problem A7
Hvorfor har 0.6 0.2 det samme svar som 6 2?

i denne del: oversættelse af processen til decimaler
du kan også udvide det, du har lært om operationer og brøker, til decimaler. Husk, at en terminerende decimal kan betragtes som en brøkdel med en effekt på 10 som nævneren (f.eks. 0,4 = 4/10). Se Note 5 nedenfor.

hvorfor skal vi stille decimalerne op, når vi tilføjer eller trækker decimaler?
vi er nødt til at stille decimalpunkterne op, fordi vi kun kan tilføje eller trække fra, hvis enhederne er de samme. Ved at justere decimalpunkterne sørger vi for, at vi tilføjer eller trækker cifre, der har de samme stedværdier, ligesom vi gør, når vi tilføjer eller trækker hele tal.

hvorfor tæller vi decimaler, når vi multiplicerer decimaler?
fra afsnittet om eksponenter i Session 3 ved vi, at multiplikation med eksponenter kræver tilføjelse eller “tælling” af eksponenterne. Så for eksempel er 0,2 * 0,03 i den eksponentielle form følgende:

0.2 • 0.03 = 2/10 • 3/100 = 2 •10-1 • 3 • 10-2

eksponenterne er -1 og -2, som er henholdsvis et og to steder til højre for decimaltegnet. Produktet vil derefter have en eksponent, der er summen af -1 og -2 (dvs.-3), og er tre steder til højre for decimaltegnet. Produktet af 0,2 * 0,03 er 0.006:

0.2 • 0.03 = 6 • 10-3 = 0.006

hvorfor flytter vi decimalerne, når vi deler med decimaler?
denne proces er relateret til at finde ækvivalente fraktioner. Du kan tænke på divisionen som en brøkdel. Siden problemet 2.5 0.05 er svært at visualisere, skriv det som 2,5/0,05. Du har brug for et helt tal i nævneren, så multiplicer med 100 for at få et helt tal. For at kompensere for at multiplicere nævneren med 100, skal du også multiplicere tælleren med 100. Det betyder, at du faktisk ganget med 100/100 eller 1, hvilket ikke ændrer værdien af fraktionen. Sådan ser processen ud: